Minimum, Maximum, Slew Rate, Discrete Difference, and Mean Signal Operators
Minimum and Maximum
The minimum and maximum operators displays the minimum and maximum value on the specified interval.
Arithmetic Mean
This operator computes the arithmetic mean of the curve on the selected range. It is computed
with the following formula (trapezoid approximation):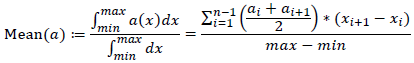
In the formula, n is the number of points of the curve in the selected range, and
ai is the value of each of these points.
Rectified Mean
This operator computes the average rectified mean of the curve on the selected range. It is
computed by taking the mean value of the absolute values: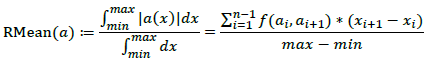
The function f takes the average of the absolute values and if both values have the same
sign it is just 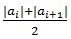 , and if they have different sign:
, and if they have different sign: 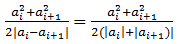 . The reason for the complex formula is to ensure that any piece-wise linear signal
(including triangular waves) is correct.
. The reason for the complex formula is to ensure that any piece-wise linear signal
(including triangular waves) is correct.
Root Mean Square (RMS)
In the case of a set of n values {x1, x2, x3,..., xn} representing the values of the point of the curve, the RMS (Root Mean Square) value is given by this formula: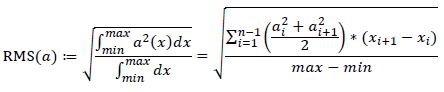
Note that for the important case of equidistantly sampled sine signal (with arbitrary phase) this formula gives the exact result (below the Nyquist frequency, and if the simulated interval is a multiple of the period of the sine signal).
AC Coupled RMS
This property is related to the standard deviation in the statistics and can be computed in two
different steps. (The first step is used to avoid numerical issues with round-off and
overflow):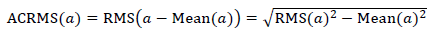
Slew Rate
The slew rate operator computes the maximum derivative value of the curve on the specified interval.
Discrete Difference
The discrete difference operator computes the discrete difference of a signal, defined as y(i)=u(i)-u(i-1).
Moving Average
This signal operator is similar to the arithmetic mean signal operator above. Comparing with the first formula for that signal operator above, to get the value at x2, we change “Mean(a)” to “Mean(a, x2)”. In the integrations we change “min” to “x2-w/2”, “max” to “x2+w/2”. Finally, instead of integrating “a(x)”, we change to integrating “a(x)/w” where w is the width of the moving average “window”.
In general, the signal operator is implemented as a Centered Moving Average. If any endpoint is missing for the calculation, it is calculated by interpolation.