Product Position Mechanism

By default, the position is defined on the product instance, using the matrix of the instance. The occurrence position is computed with a multiplication of the matrices of its parent instances.

On an assembly, you can modify the position of:

  • All occurrences: by modifying their instance position
  • One occurrence only: by overloading the occurrence position.

    For this, the reference must allow this modification (the reference must be defined as flexible) and the instance must be repositionable.

    For example, if you want to modify the position of one wheel, the axle reference and the wheel instance must allow this modification: the axle reference must be flexible, and the wheel instance must be repositionable.

This page discusses:

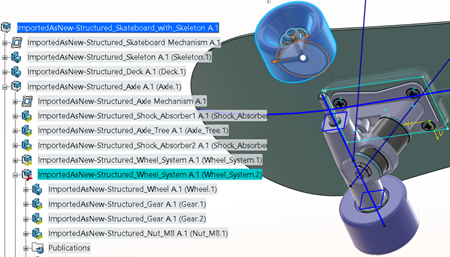
Position Matrix (Instance)

The instance position is relative to the parent reference.

A position matrix is an entity defined by twelve floats, for example:

[0] [3] [6] [9]

[1] [4] [7] [10]

[2] [5] [8] [11]

  • Coefficients from 0 to 8 define the rotation matrix(3x3). There is no unit.
  • Coefficients from 9 to 11 define the translation vector (x, y, z). The translation vector is saved in meters.

The position matrix correspond to rigid transformation that preserves orientation.

The identity position matrix (the rotation matrix is equal to identity and the translation is null) signifies that there is no move between the parent reference product and the instantiated product.

The rotation matrix must be a direct isometry. The indirect isometry (reflection) is not allowed.

An instance position can be fixed, to forbid the edition of this instance position.

Absolute Position (Occurrence)

The absolute position of an occurrence is the multiplication of the matrices of the parent instances. The absolute position is relative to the global coordinate system of the assembly.

Note: The absolute position of an occurrence can be overloaded. When the matrix of an occurrence is not identical to the matrix of its instance, the occurrence position is overloaded.

Flexibility for Overloaded Position

You can overload the position of an occurrence in the context of an assembly if the following conditions are fulfilled:

  • All the parent references must be defined as flexible (all the levels except the root).
    Note: The flexibility is applied to the parent reference. A flexible product is a multicomponent product whose components are allowed to move relatively to each other after the product has been instantiated into a larger product.
  • The instance must be defined as repositionable.
    Note: A fixed instance is independent of the occurrence position. If an instance is fixed and repositionable, you can still move an occurrence of this instance.

Example

In this example, the position of Wheel_System A.1 (Wheel_System.2) must be changed. For this:

  • The subassembly Axle A.1 is defined as flexible in a new tab.
  • The occurrence Wheel_System A.1 (Wheel_System.2) is defined as repositionable.
Note: The main root is not modified.
Image 1
You can then modify the position of this occurrence.
Image 2