Design Sensitivity Analysis Overview

A design response refers to a physical quantity of interest; for example, the displacement at a specific point or the maximum stress for a part that may be one of the key performance indicators for the part during its application. During the design of the part, you may be interested in optimizing (minimizing, maximizing, or setting constraints on) one or more design responses. A design variable, on the other hand, refers to a physical quantity (such as the thickness of shells for various regions of a shell structure or the radius of individual beams in a lattice structure) that you can modify to ensure optimum values for one or more design responses. A design sensitivity refers to the derivative of a design response with respect to a design variable. Therefore, a design sensitivity provides guidance for modifying a design variable with the objective of improving a design response, thereby improving the service performance of a part. In other words, a design sensitivity tells you in which "direction" and by "how much" you should modify the design variable (for example, should a shell thickness be decreased or increased and by what amount?) to obtain improved performance.

Figure 1 illustrates two examples of how sensitivities guide modifications of design variables to improve the structural performance of stress and eigenfrequency (design) responses, respectively, of a part. As the figure shows, the sensitivities represent linearized first-order derivatives at a given value of the design variable. Typically, sensitivities are used to iteratively modify a given design configuration to improve the structural performance. Such design modifications can be done manually or in an automated manner using optimization algorithms based upon mathematical programming. The focus here is not on the optimization algorithms but on various methods for obtaining the sensitivities. You can find examples of various optimization algorithms in the Tosca or Isight documentation.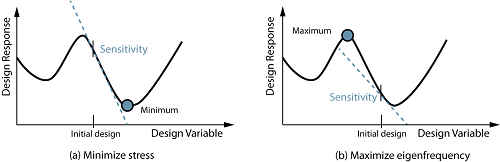

Practically, the approaches for computing design sensitivities can be classified as finite difference–based sensitivity approaches and analytical and semi-analytical sensitivity approaches. These approaches are further classified as follows:

Finite difference–based sensitivity approaches

Forward finite difference.
Backward finite difference.
Central finite difference.

Analytical and semi-analytical sensitivity approaches

Direct approach.
Adjoint approach.

Finite difference approaches are very general methods for estimating the sensitivities. Although the finite difference–based sensitivities are often not particularly accurate, they can be computed very efficiently for finite element models having a small number of design variables (< 5–10). These methods are also easy to implement. Typically, sensitivities computed using finite difference methods are applied in Isight-based optimization workflows.

The analytical and semi-analytical design sensitivity analysis approaches in Abaqus are designed for the class of problems having a medium number (> 5 but < 50–1000) to a large number (>> 1,000–1.0×10⁸) of either design variables or design responses. Direct sensitivity analysis is recommended for problems having a medium to large number of design responses but a small number of design variables (see Direct Design Sensitivity Analysis). Adjoint sensitivity analysis is recommended for problems having a large number of design variables but a small to medium number of design responses (see Adjoint Design Sensitivity Analysis).

For the class of problems that involve a medium to a large number of both design variables and design responses, no general solution for computing design sensitivities in an efficient manner exists today. However, for such problems, the number of design responses can sometimes be significantly reduced by replacing a large group of design responses of a certain type with the maximum, the minimum, or the average value over that group.