Axisymmetric elemental cavity radiation view factor calculations

These examples verify the use of axisymmetric elemental cavity radiation view factor calculations in Abaqus.

This page discusses:

Parallel circular disks with centers along the same normal
Two concentric cylinders of same finite length
Concentric cylinders of infinite length
Coaxial right circular cylinders of different radii, one on top of the other

ProductsAbaqus/Standard

Relatively simple configurations were selected for these verification problems to ensure that analytical solutions or tabulated results could be found. In some cases certain parameters such as the distance between two surfaces or the number of elements on a surface were varied to illustrate the effects of these parameters on view factor calculations within Abaqus. To duplicate the tabulated results for the cases where parameters were varied, the user can modify the input files provided with the Abaqus release.

Parallel circular disks with centers along the same normal

Problem description

Analytical solution

\begin{matrix} F ​_{1 - 2} & ​ = \frac{1}{2} (X - \sqrt{X^{2} - 4 {(\frac{R_{2}}{R_{1}})}^{2}}) \\ and \\ F ​_{2 - 1} & ​ = \frac{1}{4} F ​_{1 - 2}, \end{matrix}

where $R_{1} = r_{1} / a$ , $R_{2} = r_{2} / a$ , and $X = 1 + \frac{1 + R_{2}^{2}}{R_{1}^{2}}$ .

Results and discussion

The number of elements along the bottom area can be varied to obtain the following results:


# of elements on bottom plane	F $_{1 - 2}$		F $_{2 - 1}$
# of elements on bottom plane	Abaqus	Analytical	Abaqus	Analytical
1	0.6853	0.6800	0.1713	0.1700
2	0.6836	0.6800	0.1709	0.1700
4	0.6820	0.6800	0.1705	0.1700

Input files

xrvda4n1_1elem.inp: DCAX4 elements are used to discretize the surfaces of the cavity; one element for the top surface and one element for the bottom surface.

xrvda4n1.inp: DCAX4 elements are used to discretize the surfaces of the cavity; one element for the top surface and two elements for the bottom surface.
xrvda4n1_4elem.inp: DCAX4 elements are used to discretize the surfaces of the cavity; one element for the top surface and four elements for the bottom surface.

References

Siegel, R., and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington, 3rd, 1992.

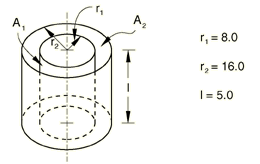
Two concentric cylinders of same finite length

Problem description

Analytical solution

F ​_{2 - 1} = \frac{1}{R} - \frac{1}{π R} (\arccos \frac{B}{A} - \frac{1}{2 L} [\sqrt{{(A + 2)}^{2} - {(2 R)}^{2}} \arccos \frac{B}{R A} + B \arcsin \frac{1}{R} - \frac{π A}{2}]),

and

\begin{matrix} F ​_{2 - 2} & ​ = 1 - \frac{1}{R} + \frac{2}{π R} \arctan \frac{2 \sqrt{R^{2} - 1}}{L} \\ - \frac{L}{2 π R} (\frac{\sqrt{{(2 R)}^{2} + L^{2}}}{L} \arcsin \frac{4 (R^{2} - 1) + (L^{2} / R^{2}) (R^{2} - 2)}{L^{2} + 4 (R^{2} - 1)} \\ - \arcsin \frac{R^{2} - 2}{R^{2}} + \frac{π}{2} [\frac{\sqrt{{(2 R)}^{2} + L^{2}}}{L} - 1]), \end{matrix}

where for any argument $θ$ , $- \frac{π}{2} \leq \arcsin θ \leq \frac{π}{2}$ , and $0 \leq \arccos θ \leq π$ ; and where $R = r_{2} / r_{1}$ , $L = l / r_{1}$ , $A = L^{2} + R^{2} - 1$ , and $B = L^{2} - R^{2} + 1$ .

Results and discussion


F $_{2 - 1}$		F $_{2 - 2}$
Abaqus	Analytical	Abaqus	Analytical
0.1645	0.1626	0.0954	0.0925

Input files

xrvda4n2.inp: One DCAX4 element is used to discretize each surface of the cavity.

References

Siegel, R., and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington, 3rd, 1992.

Concentric cylinders of infinite length

Problem description

Analytical solution

\begin{matrix} F ​_{1 - 2} & ​ = 1.0, \\ F ​_{2 - 1} & ​ = \frac{r_{1}}{r_{2}}, \\ and \\ F ​_{2 - 2} & ​ = 1 - \frac{r_{1}}{r_{2}} . \end{matrix}

Results and discussion

The number of elements on each face can be increased to obtain the additional results:


# of elements	F $_{1 - 2}$		F $_{2 - 1}$		F $_{2 - 2}$
# of elements	Abaqus	Analytical	Abaqus	Analytical	Abaqus	Analytical
4	0.9979	1.0000	0.4990	0.5000	0.4895	0.5000
8	0.9998	1.0000	0.4999	0.5000	0.4998	0.5000

Input files

xrvda4p3.inp: Four DCAX4 elements are used to discretize each surface of the cavity. The infinite extent of the cavity is modeled by repeating the elements in the z-direction using periodic symmetry (NR = 10).
xrvda4p3_8elem.inp: Eight DCAX4 elements are used to discretize each surface of the cavity. The infinite extent of the cavity is modeled by repeating the elements in the z-direction using periodic symmetry (NR = 10).

References

Siegel, R., and J. R. Howell, Thermal Radiation Heat Transfer, Hemisphere Publishing Corporation, Washington, 3rd, 1992.

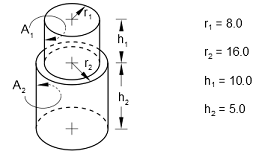
Coaxial right circular cylinders of different radii, one on top of the other

Problem description

Analytical solution

If $\frac{h_{2}}{h_{1}} \leq \frac{1}{2} (\frac{r_{2}}{r_{1}} - 1)$ and $r_{2} > r_{1}$ ,

F ​_{1 - 2} = \frac{1}{4 H_{1}} (1 - L_{2} + \sqrt{{(1 + L_{2})}^{2} - 4 R^{2}}),

where $R = r_{2} / r_{1}$ , $H_{n} = h_{n} / r_{1}$ , and $L_{n} = \frac{r_{2}^{2} + h_{n}^{2}}{r_{1}^{2}} = R^{2} + H_{n}^{2}$ .

Results and discussion


F $_{1 - 2}$
Abaqus	Analytical
0.0502	0.0446

Input files

xrvda4n4.inp: DCAX4 elements are used to discretize the surfaces of the cavity; two elements for the top area, and one element for the bottom area.

References

Howell, J. R., A Catalog of Radiation Configuration Factors, McGraw-Hill Book Company, New York, 1982.