Kinematic Coupling Constraints

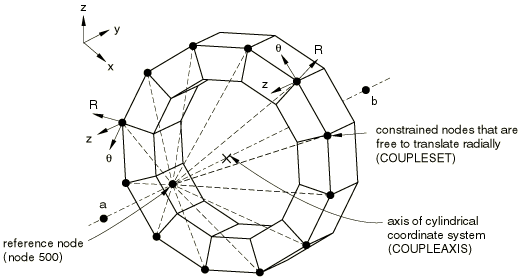
The kinematic coupling constraints are useful in cases where a large number of nodes (the “coupling” nodes) are constrained to the rigid body motion of a single node and the degrees of freedom that participate in the constraint are selected individually in a local coordinate system. In many such cases MPCs either are not available or must be prescribed individually for each constrained node. A typical example is shown in Figure 1, where a kinematic coupling constraint is used to prescribe a twisting motion to a model without constraining radial motions. In other applications the kinematic coupling constraint can be used to provide coupling between continuum and structural elements.

A kinematic coupling constraint used to transmit rotation to a structure while permitting radial motion.

A kinematic coupling constraint requires the specification of a reference node, coupling nodes, and the constrained degrees of freedom at these nodes. The reference node has both translational and rotational degrees of freedom.

Kinematic constraints are imposed by eliminating degrees of freedom at the coupling nodes. Once any combination of displacement degrees of freedom at a coupling node is constrained, additional displacement constraints—such as MPCs, boundary conditions, or other kinematic coupling definitions—cannot be applied to any coupling node involved in a kinematic coupling constraint. The same limitation applies for rotational degrees of freedom.

In geometrically nonlinear analysis steps, the coordinate system in which the constrained degrees of freedom are specified rotate with the reference node regardless of whether the constrained degrees of freedom are specified in the global coordinate system or in a local system. Thus, the constraint shown in Figure 1 will enable free radial motion throughout arbitrary rotations of the structure. Radial motion in this case is defined as motion normal to the structure's axis (defined in the undeformed configuration by points a and b in the figure), with this axis rotating with the reference node. Therefore, the free radial expansion shown in Figure 1 will not refer to an axis parallel to the global y-axis for general rotations of the reference node but will refer to an axis that rotates with the structure. Rotation of the constraint directions is not affected by the selection of the constrained degrees of freedom.

In Abaqus/Standard a kinematic coupling can experience expansion due to a temperature increase. Each coupled node expands along the line that joins the node to the reference node. The magnitude of the expansion depends on the distance of the coupled node from the reference node. The temperature change for computing the expansion is the average of the temperature change at the node and the temperature change at the reference node. The temperature change at any node is the difference between the initial temperature of the node and the current temperature of the node. You must provide the value of the thermal expansion coefficient so that Abaqus/Standard can compute the expansion.