EULER

Description

Figure 1. Connection type EULER.

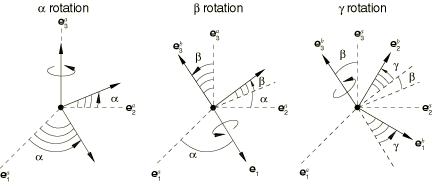
The EULER connection does not impose kinematic constraints. An EULER connection is a finite rotation connection where the local directions at node b are parameterized in terms of Euler angles relative to the local directions at node a. Local directions $\left\{{\mathbf{e}}_1^b,{\mathbf{e}}_2^b,{\mathbf{e}}_3^b\right\}$ are positioned relative to $\left\{{\mathbf{e}}_1^a,{\mathbf{e}}_2^a,{\mathbf{e}}_3^a\right\}$ by three successive finite rotations $\alpha$, $\beta$, and $\gamma$ as follows:

1. Rotate by $\alpha$ radians about axis ${\mathbf{e}}_3^a$;

2. Rotate by $\beta$ radians about the intermediate 1-axis, ${\mathbf{e}}_1=\cos \alpha {\mathbf{e}}_1^a+\sin \alpha {\mathbf{e}}_2^a$;

3. Rotate by $\gamma$ radians about axis ${\mathbf{e}}_3^b$.

The Euler angles are determined by the local directions as

Here i, j, and k are integers that account for rotations with magnitudes greater than $\pi$. Initially, the intermediate rotation angle $\beta$ is chosen in the interval $0\le \beta \le \pi$.

If the intermediate rotation is an even multiple of $\pi$, $\beta =2m\pi$, where $m=0,\pm 1,\pm 2,\mathrm{\dots }$, the other two Euler angles become non-unique. In this case

Similarly, if the intermediate rotation is an odd multiple of $\pi$, $\beta =\left(2m+1\right)\pi$, where $m=$ 0, $\pm 1,\pm 2,\mathrm{\dots }$, the other two Euler angles become nonunique as well. In this case

In both of these cases a singularity results in the rotation parameterization when the ${\mathbf{e}}_3^a$ and ${\mathbf{e}}_3^b$ axes align. The EULER connection should be used in such a way that these axes do not align throughout the computation. For a singularity-free condition Abaqus will choose $\alpha$ and $\gamma$ such that a smooth parameterization results for the above values of the intermediate angle $\beta$.

The available components of relative motion in the EULER connection are the changes in the Euler angles that position the local directions at node b relative to the local directions at node a. Therefore,

where ${\alpha }_0$, ${\beta }_0$, and ${\gamma }_0$ are the initial Euler angles. The connector constitutive rotations are

The kinetic moment in a EULER connection is determined from the three component relationships:

Summary