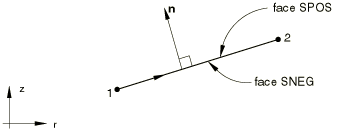
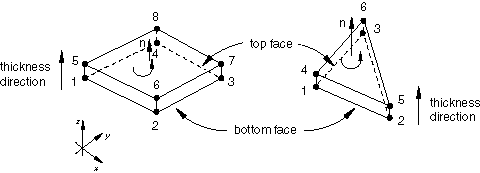
Conventional Shell Versus Continuum Shell
Shell elements are used to model structures in which one dimension, the thickness, is significantly smaller than the other dimensions. Conventional shell elements use this condition to discretize a body by defining the geometry at a reference surface. In this case the thickness is defined through the section property definition. Conventional shell elements have displacement and rotational degrees of freedom.
In contrast, continuum shell elements discretize an entire three-dimensional body. The thickness is determined from the element nodal geometry. Continuum shell elements have only displacement degrees of freedom. From a modeling point of view continuum shell elements look like three-dimensional continuum solids, but their kinematic and constitutive behavior is similar to conventional shell elements.
Figure 1 illustrates the differences between a conventional shell and a continuum shell element.