Smoothing Contact Surfaces in Abaqus/Standard

With the finite element method, curved geometric surfaces are naturally approximated as a faceted group of connected element faces. This section discusses methods to improve faceted surface representations for purposes of contact computations based on knowledge of idealized initial surface geometry. Other types of surface smoothing are discussed in Smoothing Main Surfaces for the Finite-Sliding, Node-to-Surface Formulation and Using the Small-Sliding Tracking Approach.

The use of a faceted surface geometry rather than the true surface geometry can significantly contribute to contact stress inaccuracy in contact interactions, especially when the magnitude of the differences between the faceted and true surface is not small with respect to the deformation of the components in contact. Contact stress output is of primary importance in many applications; for example, the distribution of contact pressures can be used to identify wear patterns and peak pressure values to determine relative lives of machine parts.

Abaqus/Standard offers techniques to improve the accuracy and robustness of contact computations based on comparisons between the initial faceted geometry and a more idealized initial geometry of the same surface. In some cases you may know that the idealized surface is (exactly or approximately) cylindrical, spherical, or toroidal. When creating finite element models as CAD representations in the 3DEXPERIENCE platform, idealized surface representations are often available for selection.

This page discusses:

Smoothing of Common Curved Surface Geometries
Smoothing of Faceted Surfaces Based on Comparison to CAD Representations
Considerations for Smoothing Methods Based on Knowledge of Idealized Initial Geometry

Smoothing of Common Curved Surface Geometries

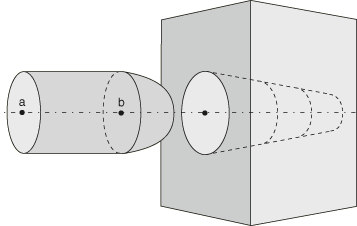
One method of surface smoothing applies to surface regions that are roughly axisymmetric, roughly spherical, or part of a toroidal surface. The smoothing method applies to general contact and surface-to-surface contact pairs. For example, the pin insertion model in Figure 1 could benefit from this smoothing: the body of the pin is cylindrical, the head of the pin is hemispherical, and the hole is conical. Surface-to-surface contact smoothing would also be effective if the surfaces were not perfectly axisymmetric, spherical, or toroidal; for example, if the pin body were slightly elliptical.

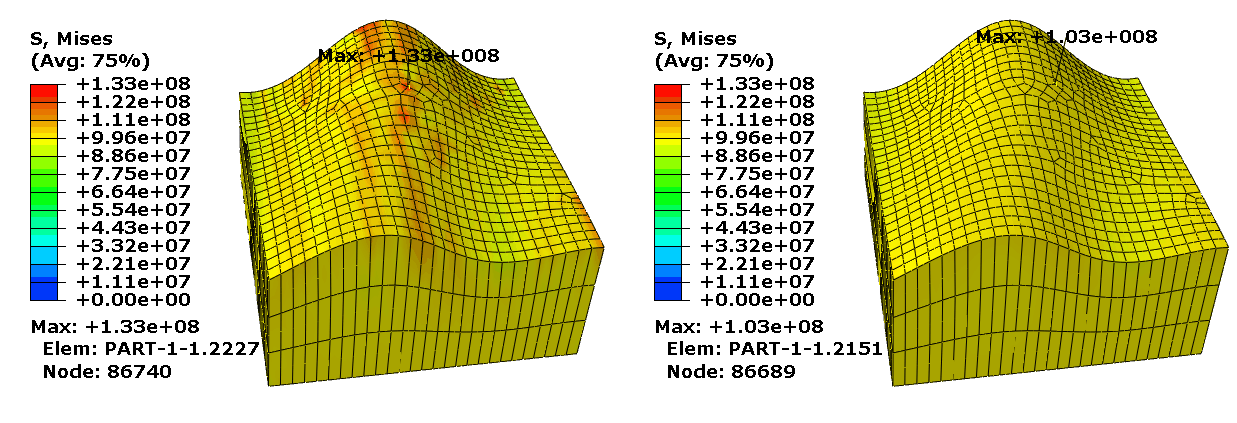
Effects of Contact Surface Smoothing

The impact of contact smoothing based on comparison of initial faceted surface geometry to initial idealized surface geometry can be demonstrated by a simple model. Figure 2 shows the initial mesh geometry for a two-dimensional model of concentric cylinders with an interference fit. The concentric cylinders are modeled with first-order elements of different sizes.

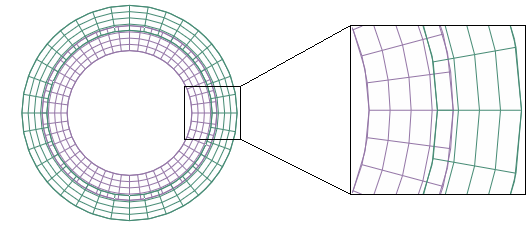
Discrepancies between the true surface geometry and the faceted surface geometry result in noise in the contact pressure solution if surface smoothing is not used. If the interference distance and resulting deformation distance is small with respect to the geometry discrepancy, this noise can have a significant effect on the accuracy of the solution. Although surface-to-surface contact typically handles these discrepancies better than node-to-surface contact, it is not unusual for the maximum deviation from the analytical pressure solution to be upward of 100%. The effects of the noise become less apparent for larger deformations, but they are never completely eliminated.

Applying Smoothing of Common Curved Surface Geometries to General Contact

Smoothing of common curved surface geometries for general contact is enabled by surface property assignments. Surface property assignments specify which surfaces are to be smoothed and the smoothing method to be used. The underlying geometry correction methods are the same for general contact and contact pairs:

The circumferential smoothing method is applicable to surfaces approximating a portion of a circle in two dimensions or a portion of a surface of revolution in three dimensions.
The spherical smoothing method is applicable to surfaces approximating a portion of a sphere in three dimensions.
The toroidal smoothing method is applicable to surfaces approximating a portion of a torus in three dimensions (i.e., a circular arc revolved about an axis).

For each surface, you must specify the appropriate geometry correction method and either the approximate axis of revolution (for circumferential or toroidal smoothing) or the approximate spherical center (for spherical smoothing). For toroidal smoothing, you must also specify the distance of the center of the circular arc from the axis of revolution, and the line joining point (X_a, Y_a, Z_a) and the center of the circular arc should be perpendicular to the axis of revolution.

Example: Pin-in-Hole with General Contact

To improve contact pressure accuracy for the model in Figure 1, contact smoothing can be applied to both the main and secondary surfaces. Two different geometric correction methods are required for the pin (the secondary surface), so additional surfaces are defined corresponding to regions of the secondary surface. Spherical smoothing is defined for the tip of the pin. Since the body of the pin and the hole share an axis of revolution, circumferential smoothing is applied to both of these surfaces. This surface smoothing definition applies even if the cross-sectional shapes of the pin and hole deviate from perfect circles.

SURFACE INTERACTION, NAME=FRICTION1
CONTACT
CONTACT INCLUSIONS
PIN, HOLE
CONTACT PROPERTY ASSIGNMENT
 , , FRICTION1
SURFACE PROPERTY ASSIGNMENT, PROPERTY=GEOMETRIC CORRECTION, DEFINITION=COORDINATES
PIN_TIP, SPHERICAL, X_b, Y_b, Z_b
PIN_BODY, CIRCUMFERENTIAL, X_a, Y_a, Z_a, X_b, Y_b, Z_b
HOLE, CIRCUMFERENTIAL, X_a, Y_a, Z_a, X_b, Y_b, Z_b

Applying Smoothing of Common Curved Surface Geometries to Surface-to-Surface Contact Pairs

Smoothing of common curved surface geometries for contact pairs that use a surface-to-surface contact formulation is enabled by creating a surface smoothing definition. A contact pair definition references this smoothing definition to apply geometric corrections in the contact formulation (the physical geometry of the model is not altered).

The surface smoothing definition lists all of the faceted regions in the contact pair surfaces that must be smoothed, as well as the geometry correction method that should be applied to each region. Three geometry correction methods can be employed:

The circumferential smoothing method is applicable to surfaces approximating a portion of a circle in two dimensions or a portion of a surface of revolution in three dimensions.
The spherical smoothing method is applicable to surfaces approximating a portion of a sphere in three dimensions.
The toroidal smoothing method is applicable to surfaces approximating a portion of a torus in three dimensions (i.e., a circular arc revolved about an axis).

Each surface-to-surface contact pair refers to a single smoothing definition; therefore, a smoothing definition must list all of the smoothed regions and applicable geometry correction methods for the contact pair. Geometry corrections can be applied to main surfaces and to secondary surfaces; you can also apply corrections to selected regions of each surface. A surface smoothing definition can include multiple regions and different geometric correction methods for each region. For each region, you must specify the appropriate geometry correction method and either the approximate axis of revolution (for circumferential or toroidal smoothing) or the approximate spherical center (for spherical smoothing). For toroidal smoothing, you must also specify the distance of the center of the circular arc from the axis of revolution, and the line joining point (X_a, Y_a, Z_a) and the center of the circular arc should be perpendicular to the axis of revolution.

Example: Pin-in-Hole with Contact Pairs

CONTACT PAIR, TYPE=SURFACE TO SURFACE, INTERACTION=FRICTION1, 
   GEOMETRIC CORRECTION=SMOOTH1
PIN, HOLE
SURFACE INTERACTION, NAME=FRICTION1
SURFACE SMOOTHING, NAME=SMOOTH1
PIN_TIP, , SPHERICAL, X_b, Y_b, Z_b
PIN_BODY, HOLE, CIRCUMFERENTIAL, X_a, Y_a, Z_a, X_b, Y_b, Z_b

Smoothing of Faceted Surfaces Based on Comparison to CAD Representations

Simulations using general contact submitted from 3DEXPERIENCE platform Scenario Creation apps can use a technique to improve finite element representations of contact surfaces. This technique is based on deviations of the original element-based surface geometry from a more accurate reference representation of the undeformed geometry and leverages CAD surface representations available in the 3DEXPERIENCE platform in the computation of contact geometry corrections. This technique is not available in explicit dynamic steps.

The CAD-based smoothing method is applicable to arbitrary surface shapes having CAD representations in the 3DEXPERIENCE platform. Consider the example shown in Figure 3. This example is constructed such that the analytical solution has a uniform, uniaxial stress state of 10⁸ Pa. The curved contact interface has closed contact and sticking friction everywhere, and the same elastic material exists on both sides of the contact interface. The meshes used in this example are made of quadratic hexahedral and wedge elements. The meshes do not have matched nodes across the contact interface, which causes significant stress noise if the contact surfaces are not smoothed, especially for small strains where the level of element deformation is less than or equal to the distances associated with the mismatch of faceted surface representations across the interface.

Figure 4 shows that CAD-enhanced contact reduces stress noise for this example. For example, the maximum Mises stress deviates from the analytical Mises stress solution by 33% without CAD-enhanced contact, and this deviation is less than 3% with CAD-enhanced contact. The CAD-based smoothing also significantly improves contact pressure results for this model.

Considerations for Smoothing Methods Based on Knowledge of Idealized Initial Geometry

The smoothing methods in this section are used to adjust contact penetration/gap computations based on differences in undeformed geometries between faceted finite element surface representations and more idealized surface representations. The effects of the surface smoothing techniques discussed in this section tend to be most significant for analyses involving small deformation and coarse mesh discretization with first-order elements in the contact region; however, significant improvements to contact stress solutions are common even when the mesh is quite refined or higher-order elements are used. For analyses with large deformation these smoothing techniques typically have an insignificant effect on solutions. However, in some cases the smoothing can degrade the solution accuracy after large deformation; therefore, it is not recommended to use these smoothing techniques for large-deformation analyses. The effectiveness of the smoothing does not degrade upon relative motion between contact surfaces; for example, the smoothing technique works well for cases involving large sliding but small deformation.

The surface smoothing techniques discussed in this section assume that initial locations of surface nodes lie on the true initial surface geometry, with the exception of midside nodes of higher-order elements. These smoothing techniques remain effective even if the midside nodes of higher-order elements do not lie on the true initial geometry.