Plasticity Model for Bidirectional Fabric-Reinforced Composite Materials

The shear plasticity model provided in Abaqus/Explicit is intended for modeling the nonlinear in-plane shear behavior of the matrix of bidirectional fabric-reinforced composite materials. In Abaqus/Explicit the elastic behavior for bidirectional fabric-reinforced composites is assumed to be in the form of bilamina elasticity (see Defining Orthotropic Elasticity in Plane Stress with Different Moduli in Tension and Compression). This shear plasticity model can be used with the ply fabric damage initiation criterion (see Ply Fabric Criterion) to simulate progressive damage and failure for bidirectional fabric-reinforced composites.

This page discusses:

Shear Plasticity Behavior
Elements

Shear Plasticity Behavior

The shear plasticity model of the matrix is formulated in the local directions of the bidirectional fabric-reinforced material and is assumed to be decoupled from the response along the local 1 and 2 fiber directions. The following elastic relation gives the in-plane shear stress in terms of the elastic shear strain, $ε_{12}^{e l}$ :

σ_{12} = 2 G_{12} ε_{12}^{e l} = 2 G_{12} (ε_{12} - ε_{12}^{p l}),

where $G_{12}$ is the shear modulus of the matrix, $ε_{12}$ is the total shear strain, and $ε_{12}^{p l}$ is the plastic shear strain.

The yield surface and flow rule are defined as:

F = | σ_{12} | - \bar{σ} ({\bar{ε}}^{p l}, {\dot{\bar{ε}}}^{p l}) = 0,

{\dot{ε}}^{p l} = {\dot{\bar{ε}}}^{p l} \frac{\partial F}{\partial σ_{12}},

where $\bar{σ}$ is the yield stress, ${\bar{ε}}^{p l}$ is the equivalent plastic strain, and ${\dot{\bar{ε}}}^{p l}$ is the equivalent plastic strain rate.

The hardening behavior and strain rate dependency are incorporated into the yield stress $\bar{σ}$ assuming this separable form:

\bar{σ} ({\bar{ε}}^{p l}, {\dot{\bar{ε}}}^{p l}) = σ^{0} ({\bar{ε}}^{p l}) R ({\dot{\bar{ε}}}^{p l}),

where $σ^{0}$ is the static yield stress, and $R$ is a ratio, defined as $R = 1.0$ at ${\dot{\bar{ε}}}^{p l} = 0.0$ .

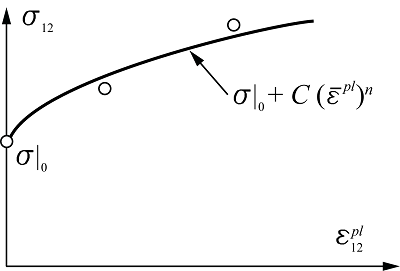
The hardening behavior defines the evolution of the yield surface size, $σ^{0}$ , as a function of the equivalent plastic strain, ${\bar{ε}}^{p l}$ . This evolution can be introduced by specifying $σ^{0}$ directly as a function of ${\bar{ε}}^{p l}$ in tabular form or by using the Johnson-Cook law:

σ^{0} = {σ |}_{0} + C {({\bar{ε}}^{p l})}^{n},

where ${σ |}_{0}$ is the yield stress at zero plastic strain and $C$ and $n$ are material parameters. A schematic figure of the hardening curve based on the Johnson-Cook law is shown in Figure 1.

You can specify rate-dependent effects using the Cowper-Symonds overstress power law form or the Johnson-Cook form. For more information on these methods, see Rate-Dependent Yield.

Input File Usage

Use the following option to define Johnson-Cook hardening behavior:

PLY FABRIC HARDENING, TYPE=JOHNSON COOK (default)

Use the following option to define the hardening behavior by giving the yield stress as a function of the yield strain:

PLY FABRIC HARDENING, TYPE=TABULAR

Use both of the following options to specify rate-dependent effects:

PLY FABRIC HARDENING (to specify the static yield stress  $σ^{0} ({\bar{ε}}^{p l})$ )
RATE DEPENDENT (to specify the ratio  $R ({\dot{\bar{ε}}}^{p l})$ )

Elements

The shear plasticity model for bidirectional fabric-reinforced composite materials can be used with elements with a plane stress formulation, which include plane stress, shell, continuum shell, and membrane elements in Abaqus/Explicit.