Moisture Swelling

The moisture swelling model assumes that the volumetric swelling of the porous medium's solid skeleton is a function of the saturation of the wetting liquid in partially saturated flow conditions. The porous medium is partially saturated when the pore liquid pressure, $u_w$, is negative (see Effective stress principle for porous media).

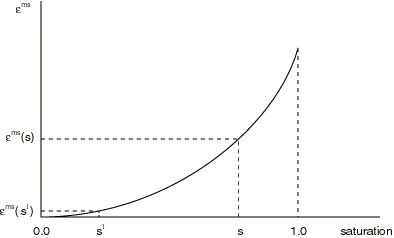
The swelling behavior is assumed to be reversible. The logarithmic measure of swelling strain is calculated with reference to the initial saturation so that

where ${\epsilon }^{ms}\left(s\right)$ and ${\epsilon }^{ms}\left(s^I\right)$ are the volumetric swelling strains at the current and initial saturations. A typical curve is shown in Figure 1. The ratios $r_{11}$, $r_{22}$, and $r_{33}$ allow for anisotropic swelling as discussed below.

Typical volumetric moisture swelling versus saturation curve.

Define the volumetric swelling strain, ${\epsilon }^{ms}$, as a tabular function of the wetting liquid saturation, s. The swelling strain must be defined for the range $0.0\le s\le 1.0$.

You can define the initial saturation values as initial conditions. If no initial saturation values are given, the default is fully saturated conditions (saturation of 1.0). For partial saturation the initial saturation and pore fluid pressure must be consistent, in the sense that the pore fluid pressure must lie within the absorption and exsorption values for the initial saturation value (see Permeability). If this is not the case, Abaqus/Standard will adjust the saturation value as needed to satisfy this requirement.

Anisotropy can be included in moisture swelling behavior by defining the ratios $r_{11}$, $r_{22}$, and $r_{33}$, such that two or more of the three ratios differ. If the ratios $r_{ii}$ are not specified, Abaqus/Standard assumes that the swelling is isotropic and that $r_{11}=r_{22}=r_{33}=1.0$. The orientation of the moisture swelling strain directions depends on the user-specified local orientation (see Orientations).