Mullins Effect

When an elastomeric test specimen is subjected to simple tension from its virgin state, unloaded, and then reloaded, the stress required on reloading is less than that on the initial loading for stretches up to the maximum stretch achieved during the initial loading. This stress softening phenomenon is known as the Mullins effect and reflects damage incurred during previous loading. This type of material response is depicted qualitatively in Figure 1.

Idealized response of the Mullins effect model.

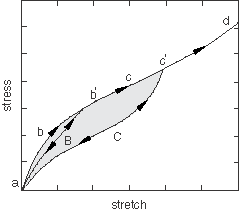
This figure and the accompanying description is based on work by Ogden and Roxburgh (1999), which forms the basis of the model implemented in Abaqus. Consider the primary loading path $ab{b}^{{}^{\prime }}$ of a previously unstressed material, with loading to an arbitrary point $b^{{}^{\prime }}$. On unloading from $b^{{}^{\prime }}$, the path $b^{{}^{\prime }}Ba$ is followed. When the material is loaded again, the softened path is retraced as $aB{b}^{{}^{\prime }}$. If further loading is then applied, the path $b^{\prime }c$ is followed, where $b^{\prime }c$ is a continuation of the primary loading path $ab{b}^{{}^{\prime }}c{c}^{{}^{\prime }}d$ (which is the path that would be followed if there was no unloading). If loading is now stopped at $c^{{}^{\prime }}$, the path $c^{{}^{\prime }}Ca$ is followed on unloading and then retraced back to $c^{{}^{\prime }}$ on reloading. If no further loading beyond $c^{{}^{\prime }}$ is applied, the curve $aC{c}^{\prime }$ represents the subsequent material response, which is then elastic. For loading beyond $c^{{}^{\prime }}$, the primary path is again followed and the pattern described is repeated.

This is an ideal representation of Mullins effect since in practice there is some permanent set upon unloading and/or viscoelastic effects such as hysteresis. Points such as $b^{{}^{\prime }}$ and $c^{{}^{\prime }}$ might not exist in reality in the sense that unloading from the primary curve followed by reloading to the maximum strain level attained earlier usually results in a stress that is somewhat lower than the stress corresponding to the primary curve. In addition, the cyclic response for some filled elastomers shows evidence of progressive damage during unloading from and subsequent reloading to a certain maximum strain level. Such progressive damage usually occurs during the first few cycles, and the material behavior soon stabilizes to a loading/unloading cycle that is followed beyond the first few cycles. More details regarding the actual behavior and how test data that display such behavior can be used to calibrate the Abaqus model for Mullins effect are discussed later and in Analysis of a solid disc with Mullins effect and permanent set.

The loading path $ab{b}^{{}^{\prime }}c{c}^{{}^{\prime }}d$ will henceforth be referred to as the “primary hyperelastic behavior.” The primary hyperelastic behavior is defined by using a hyperelastic material model.

Stress softening is interpreted as being due to damage at the microscopic level. As the material is loaded, the damage occurs by the severing of bonds between filler particles and the rubber molecular chains. Different chain links break at different deformation levels, thereby leading to continuous damage with macroscopic deformation. An equivalent interpretation is that the energy required to cause the damage is not recoverable.

Hyperelastic materials are described in terms of a “strain energy potential” function $U\left(\mathbf{F}\right)$ that defines the strain energy stored in the material per unit reference volume (volume in the initial configuration). The quantity $\mathbf{F}$ is the deformation gradient tensor. To account for Mullins effect, Ogden and Roxburgh propose a material description that is based on an energy function of the form $U\left(\mathbf{F},\eta \right)$, where the additional scalar variable, $\eta$, represents damage in the material. The damage variable controls the material properties in the sense that it enables the material response to be governed by an energy function on unloading and subsequent submaximal reloading different from that on the primary (initial) loading path from a virgin state. Because of the above interpretation of $\eta$, it is no longer appropriate to think of U as the stored elastic energy potential. Part of the energy is stored as strain energy, while the rest is dissipated due to damage. The shaded area in Figure 1 represents the energy dissipated by damage as a result of deformation until the point $c^{{}^{\prime }}$, while the unshaded part represents the recoverable strain energy.

The following paragraphs provide a summary of the Mullins effect model in Abaqus. For further details, see Mullins effect. In preparation for writing the constitutive equations for Mullins effect, it is useful to separate the deviatoric and the volumetric parts of the total strain energy density as

In the above equation U, $U_{dev}$, and $U_{vol}$ are the total, deviatoric, and volumetric parts of the strain energy density, respectively. All the hyperelasticity models in Abaqus use strain energy potential functions that are already separated into deviatoric and volumetric parts. For example, the polynomial models use a strain energy potential of the form

where the symbols have the usual interpretations. The first term on the right represents the deviatoric part of the elastic strain energy density function, and the second term represents the volumetric part.

The Mullins effect is accounted for by using an augmented energy function of the form

where ${\tilde{U}}_{dev}\left({\overline{\lambda }}_i\right)$ is the deviatoric part of the strain energy density of the primary hyperelastic behavior, defined, for example, by the first term on the right-hand-side of the polynomial strain energy function given above; ${\tilde{U}}_{vol}\left(J^{e\mathrm{\ell }}\right)$ is the volumetric part of the strain energy density, defined, for example, by the second term on the right-hand-side of the polynomial strain energy function given above; ${\overline{\lambda }}_i$$\left(i=1,2\right)$ represent the deviatoric principal stretches; and $J^{e\mathrm{\ell }}$ represents the elastic volume ratio. The function $\varphi \left(\eta \right)$ is a continuous function of the damage variable $\eta$ and is referred to as the “damage function.” When the deformation state of the material is on a point on the curve that represents the primary hyperelastic behavior, $\eta =1$, $\varphi \left(\eta \right)=0$, $U\left({\overline{\lambda }}_i,1\right)={\tilde{U}}_{dev}\left({\overline{\lambda }}_i\right)+{\tilde{U}}_{vol}\left(J^{e\mathrm{\ell }}\right)$, and the augmented energy function reduces to the strain energy density function of the primary hyperelastic behavior. The damage variable varies continuously during the course of the deformation and always satisfies $0<\eta \le 1$. The above form of the energy function is an extension of the form proposed by Ogden and Roxburgh to account for material compressibility.

With the above modification to the energy function, the stresses are given by

where $\tilde{\mathbf{S}}$ is the deviatoric stress corresponding to the primary hyperelastic behavior at the current deviatoric deformation level ${\overline{\lambda }}_i$ and $\tilde{p}$ is the hydrostatic pressure of the primary hyperelastic behavior at the current volumetric deformation level $J^{e\mathrm{\ell }}$. Thus, the deviatoric stress as a result of Mullins effect is obtained by simply scaling the deviatoric stress of the primary hyperelastic behavior with the damage variable $\eta$. The pressure stress is the same as that of the primary behavior. The model predicts loading/unloading along a single curve (that is different, in general, from the primary hyperelastic behavior) from any given strain level that passes through the origin of the stress-strain plot. It cannot capture permanent strains upon removal of load. The model also predicts that a purely volumetric deformation will not have any damage or Mullins effect associated with it.

The damage variable, $\eta$, varies with the deformation according to

where $U_{dev}^m$ is the maximum value of ${\tilde{U}}_{dev}$ at a material point during its deformation history; r, $\beta$, and m are material parameters; and $\mathrm{erf}\left(x\right)$ is the error function defined as

When ${\tilde{U}}_{dev}=U_{dev}^m$ , corresponding to a point on the primary curve, $\eta =1.0$ . However, $\eta$ attains its minimum value, ${\eta }_m$ , given by

upon removal of deformation, when ${\tilde{U}}_{dev}=0$ . For all intermediate values of ${\tilde{U}}_{dev}$ , $\eta$ varies monotonically between $1.0$ and ${\eta }_m$ . While the parameters r and $\beta$ are dimensionless, the parameter m has units of energy density (i.e., energy per unit volume), which is equivalent to stress units. The equation for $\eta$ reduces to that proposed by Ogden and Roxburgh when $\beta =0$ . The material parameters can be specified directly or can be computed by Abaqus based on curve-fitting of unloading-reloading test data. These parameters are subject to the restrictions $r>1$ , $\beta \ge 0$ , and $m\ge 0$ (the parameters $\beta$ and m cannot both be zero). Alternatively, the damage variable $\eta$ can be defined through user subroutine UMULLINS in Abaqus/Standard and VUMULLINS in Abaqus/Explicit.

If the parameter $\beta =0$ and the parameter m has a value that is small compared to $U_{dev}^m$ , the slope of the stress-strain curve at the initiation of unloading from relatively large strain levels might become very high. As a result, the response might become discontinuous, as illustrated in Figure 2.

Overly stiff response at the initiation of unloading.

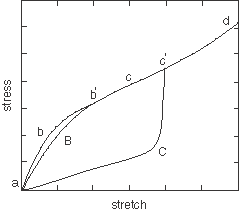
This kind of behavior might lead to convergence problems in Abaqus/Standard. In Abaqus/Explicit the high stiffness will lead to very small stable time increments, thereby leading to a degradation in performance. This problem can be avoided by choosing a small value for $\beta$ . The choice $\beta =0$ can be used to define the original Ogden-Roxburgh model. In Abaqus/Standard the default value of $\beta$ is 0. In Abaqus/Explicit, however, the default value of $\beta$ is 0.1. Thus, if you do not specify a value for $\beta$ , it is assumed to be 0 in Abaqus/Standard and 0.1 in Abaqus/Explicit.

The parameters r, $\beta$, and m do not have direct physical interpretations in general. The parameter m controls whether damage occurs at low strain levels. If $m=0$, there is a significant amount of damage at low strain levels. On the other hand, a nonzero m leads to little or no damage at low strain levels. For further discussion regarding the implications of this model to the energy dissipation, see Mullins effect. The qualitative effects of varying the parameters r and $\beta$ individually, while holding the other parameters fixed, are shown in Figure 3.

Qualitative dependence of damage on material properties.

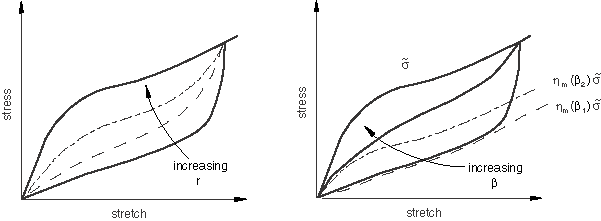
The left figure shows the unloading-reloading curve from a certain maximum strain level for increasing values of r. It suggests that the parameter r controls the amount of damage, with decreasing damage for increasing r. This behavior follows from the fact that the larger the value of r, the less the damage variable $\eta$ can deviate from unity. The figure on the right shows the unloading-reloading curve from a certain maximum strain level for increasing values of $\beta$. The figure suggests that increasing $\beta$ also leads to lower amounts of damage. It also shows that the unloading-reloading response approaches the asymptotic response given by ${\eta }_m\tilde{\sigma }$, where ${\eta }_m$ is the minimum value of $\eta$, faster for lower values of $\beta$. The dashed curves represent the asymptotic response at two different values of $\beta$ (${\beta }_1$ and ${\beta }_2$). For fixed values of r and m, ${\eta }_m$ is a function of $\beta$. In particular, if $m=0$,

The above relation is approximately true if $U_{dev}^m$ is much greater than m.

The primary hyperelastic behavior is defined by using the hyperelastic material model (see Hyperelastic Behavior of Rubberlike Materials). The Mullins effect model can be defined by specifying the Mullins effect parameters directly or by using test data to calibrate the parameters. Alternatively, you can define the Mullins effect model with user subroutine UMULLINS in Abaqus/Standard and VUMULLINS in Abaqus/Explicit.

Using Test Data to Calibrate the Parameters

Experimental unloading-reloading data from different strain levels can be specified for up to three simple tests: uniaxial, biaxial, and planar. Abaqus will then compute the material parameters using a nonlinear least-squares curve fitting algorithm. It is generally best to obtain data from several experiments involving different kinds of deformation over the range of strains of interest in the actual application and to use all these data to determine the parameters. It is also important to obtain a good curve-fit for the primary hyperelastic behavior if the primary behavior is defined using test data.

By default, Abaqus attempts to fit all three parameters to the given data. This is possible in general, except in the situation when the test data correspond to unloading-reloading from only a single value of $U_{dev}^m$ . In this case the parameters m and $\beta$ cannot be determined independently; one of them must be specified. If you specify neither m nor $\beta$ , Abaqus needs to assume a default value for one of these parameters. In light of the potential problems discussed earlier with $\beta =0$ , Abaqus assumes that $m=0$ in the above situation. The curve-fitting can also be carried out by specifying any one or two of the material parameters to be fixed, predetermined values.

As many data points as required can be entered from each test. It is recommended that data from all three tests (on samples taken from the same piece of material) be included and that the data points cover unloading/reloading from/to the range of nominal strain expected to arise in the actual loading.

The strain data should be given as nominal strain values (change in length per unit of original length). The stress data should be given as nominal stress values (force per unit of original cross-sectional area). These tests allow for entering both compression and tension data. Compressive stresses and strains are entered as negative values.

For each set of test input, the data point with the maximum nominal strain identifies the point of unloading. This point is used by the curve-fitting algorithm to compute $U_{dev}^m$ for that curve.

Figure 4 shows some typical unloading-reloading data from three different strain levels.

Typical available test data for Mullins effect.

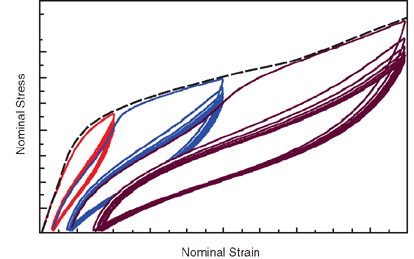
The data include multiple loading and unloading cycles from each strain level. As Figure 4 indicates, the loading/unloading cycles from any given strain level do not occur along a single curve, and there is some amount of hysteresis. There is also some amount of permanent set upon removal of the applied load. The data also show evidence of progressive damage with repeated cycling at any given maximum strain level. The response appears to stabilize after a number of cycles. When such data are used to calibrate the Mullins effect model, the resulting response will capture the overall stiffness characteristics, while ignoring effects such as hysteresis, permanent set, or progressive damage. The above data can be provided to Abaqus in the following manner:

• The primary curve can be made up of the data points indicated by the dashed curve in Figure 4. Essentially, this consists of an envelope of the first loading curves to the different strain levels.

• The unloading-reloading curves from the three different strain levels can be specified by providing the data points as is; i.e., as the repeated unloading-reloading cycles shown in Figure 4. As discussed earlier, the data from the different strain levels need to be distinguished by providing them as different tables. For example, assuming that the test data correspond to the uniaxial tension state, three tables of uniaxial test data would have to be defined for the three different strain levels shown in Figure 4. In this case Abaqus will provide a best fit using all the data points (from all strain levels). The resulting fit would result in a response that is an average of all the test data at any given strain level. While permanent set can be modeled (see Permanent Set in Rubberlike Materials), hysteresis will be lost in the process.

• Alternatively, you can provide any one unloading-reloading cycle from each different strain level. If the component is expected to undergo repeated cyclic loading, the latter might be, for example, the stabilized cycle at each strain level. On the other hand, if the component is expected to undergo predominantly monotonic loading with perhaps small amounts of unloading, the very first unloading curve at each strain level might be the appropriate input data for calibrating the Mullins coefficients.

Once the Mullins effect constants are determined, the behavior of the Mullins effect model in Abaqus is established. However, the quality of this behavior must be assessed: the prediction of material behavior under different deformation modes must be compared against the experimental data. You must judge whether the Mullins effect constants determined by Abaqus are acceptable, based on the correlation between the Abaqus predictions and the experimental data. Single-element test cases can be used to derive the nominal stress–nominal strain response of the material model.

The steps that can be taken for improving the quality of the fit for the Mullins effect parameters are similar in essence to the guidelines provided for curve fitting the primary hyperelastic behavior (see Hyperelastic Behavior of Rubberlike Materials for details). In addition, the quality of the fit for the Mullins effect parameters depends on a good fit for the primary hyperelastic behavior, if the primary behavior is defined using test data.

The quality of the fit can be evaluated by carrying out a numerical experiment with a single element that is loaded in the same mode for which test data has been provided. Alternatively, the numerical response for both the primary and the softening behavior can be obtained by requesting model definition data output (see About Output) and carrying out a data check analysis. The response computed by Abaqus is printed in the data (.dat) file along with the experimental data.