Permanent Set in Rubberlike Materials

This feature:

  • is intended for modeling permanent set observed in filled elastomers and thermoplastics;

  • is based on multiplicative split of the deformation gradient;

  • is based on the theory of incompressible isotropic hardening plasticity;

  • can be used with any isotropic hyperelasticity model;

  • can be combined with Mullins effects; and

  • cannot be used to model viscoelastic or hysteresis effects or with the steady-state transport procedure.

This page discusses:

 

See Also
Combining Material Behaviors
Hyperelastic Behavior of Rubberlike Materials
Classical Metal Plasticity
*HYPERELASTIC
*MULLINS EFFECT
*PLASTIC

Material Behavior

The real behavior of filled rubber elastomers under cyclic loading conditions is quite complex as shown in Figure 1.

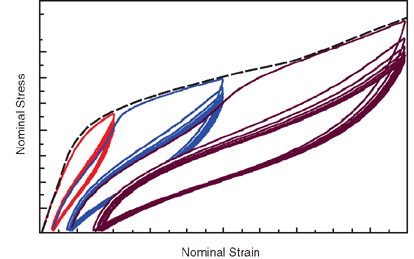
Typical behavior of a filled elastomer.

The observed mechanical behaviors are progressive damage resulting in a reduction of load-carrying capacity with each cycle, stress softening (also known as Mullins effect) upon reloading after the first unloading from a previously attained maximum strain level, hysteretic dissipation of energy, and permanent set. This section is concerned with modeling permanent set; therefore, the idealized representation of permanent set is described below.

Idealized Material Behavior

From Figure 1 it is clear that the observed permanent set is different for each cycle, but the material has a tendency to stabilize after a number of cycles of loading between zero stress and a given level of strain. For a given load level along the primary loading path shown with the dashed line in Figure 1, the idealized representation of permanent set will be a single strain value after unloading has taken place. Since rate and time effects are ignored in this model, idealized loading and unloading take place along the same path, whether Mullins effect is included or not.

The permanent set behavior is captured by isotropic hardening Mises plasticity with an associated flow rule. In the context of finite elastic strains associated with the underlying rubberlike material, plasticity is modeled using a multiplicative split of the deformation gradient into elastic and plastic components:

F=Fe⋅Fp,

where Fe is the elastic part of the deformation gradient (representing the hyperelastic behavior) and Fp is the plastic part of the deformation gradient (representing the stress-free intermediate configuration).

An example of modeling permanent set along with Mullins effect for a rubberlike material can be found in Analysis of a solid disc with Mullins effect and permanent set.

Specifying Permanent Set

The primary hyperelastic behavior can be defined by using any of the hyperelastic material models (see Hyperelastic Behavior of Rubberlike Materials). If test data input is used to define the hyperelastic response of the material, the data must be specified with respect to the stress-free intermediate configuration after unloading has taken place.

Permanent set can be defined through an isotropic hardening function in terms of the yield stress and the equivalent plastic strain. In this case the yield stress is the (effective) Kirchoff stress on the primary loading path from which unloading takes place, and the equivalent plastic strain is the corresponding logarithmic permanent set observed in the material. If σ is the true (Cauchy) stress, Kirchoff stress is defined as J⁢σ, where J is the determinant of F.

Depending on what is being modeled, permanent set may be defined as the true permanent set seen in the material after recovery of viscoelastic strains or it may include viscoelastic strains. In either case, an initial yield stress is required, below which there will be no permanent set and the behavior of the material will be fully elastic. In the case of filled rubbers this initial yield stress may correspond to a small nonzero stress; whereas for the family of thermoplastic materials, there may be a more marked value of initial yield stress.

Limitations

The model is intended to capture permanent set under multiaxial stress states and mild reverse loading conditions, as illustrated by Govindarajan, Hurtado, and Mars (2007). This model is not intended to capture deformation under complete reverse loading. Any rate effects apply only to the plastic part of the material definition.

Elements

Permanent set can be modeled with all element types that support the use of the hyperelastic material model.

Procedures

Permanent set modeling can be carried out in all procedures that support the use of the hyperelastic material model with the exception of the steady-state transport procedure. In linear perturbation steps in Abaqus/Standard, the current material tangent stiffness corresponding to the elastic part is used to determine the response, while ignoring any plasticity effects.

References

  1. Govindarajan,  S. M., J. A. Hurtado, and W. V. Mars, “Simulation of Mullins Effect in Filled Elastomers Using Multiplicative Decomposition,” European Conference for Constitutive Models for Rubber, September 2007, Paris, France.
  2. Simo,  J. C., “Algorithms for Static and Dynamic Multiplicative Plasticity that Preserve the Classical Return Mapping Schemes of the Infinitesimal Theory,” Computer Methods in Applied Mechanics and Engineering, vol. 99 61–112, 1992.
  3. Weber,  G.,  and L. Anand, “Finite Deformation Constitutive Equations and Time Integration Procedure for Isotropic Hyperelastic-Viscoplastic Solids,” Computer Methods in Applied Mechanics and Engineering, vol. 79 173–202, 1990.