Line spring elements

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

LS3S with constant-depth notch under far-field bending
LS3S with variable depth notch under far-field bending
LS6 under far-field bending
LS3S under far-field tension
LS6 under Mode I, II, and III loading

ProductsAbaqus/Standard

LS3S with constant-depth notch under far-field bending

Problem description

ELEMENT, TYPE=LS3S, ELSET=ALL
1, 2, 5, 1
SURFACE FLAW, SIDE=POSITIVE
1, .05
5, .05
2, .05
SHELL SECTION, MAT=M1, ELSET=ALL
.1,

Material:

Linear elastic, Young's modulus = 1.0, Poisson's ratio = 0.0.

Boundary conditions:

$u_{x} = u_{y} = $ 0 at nodes 1, 2, and 5.

Loading:

M ${}_{y}=$ −1.0 at nodes 1 and 2. M ${}_{y}=$ −4.0 at node 5.

Results and discussion


Element	Pt.	J	K	J_elastic
1	1	4.43 × 10⁶	2105.0	4.43 × 10⁶
1	2	4.43 × 10⁶	2105.0	4.43 × 10⁶
1	3	4.43 × 10⁶	2105.0	4.43 × 10⁶

Input files

exls3bx2.inp: Single-edge constant-depth notch strip under far-field bending.

LS3S with variable depth notch under far-field bending

Problem description

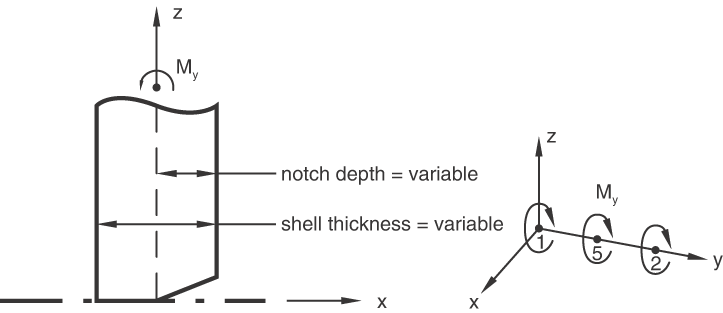
ELEMENT, TYPE=LS3S, ELSET=ALL
1, 2, 5, 1
SURFACE FLAW, SIDE=POSITIVE
1, .07
5, .05
2, .04
SHELL SECTION, MAT=M1, ELSET=ALL, NODAL THICKNESS
99,
NODAL THICKNESS
1, 0.7
5, 0.5
2, 0.4
3, 0.1
4, 0.1
6, 0.1
7, 0.1
8, 0.1

Material:

Linear elastic, Young's modulus = 1.0, Poisson's ratio = 0.0.

Boundary conditions:

$u_{x} = u_{y} = $ 0 at nodes 1, 2, and 5.

Loading:

M ${}_{y}=$ −1.0 at nodes 1 and 2. M ${}_{y}=$ −4.0 at node 5.

Results and discussion


Element	Pt.	J	K	J_elastic
1	1	6891.0	83.012	6891.0
1	2	3528.5	59.401	3528.5
1	3	1286.2	35.864	1286.2

Input files

exls3vx2.inp: Single-edge variable-depth notch strip under far-field bending.

LS6 under far-field bending

Problem description

ELEMENT, TYPE=LS6, ELSET=ALL
1, 2, 5, 1, 12, 15, 11
SURFACE FLAW, SIDE=POSITIVE
1, .05
5, .05
2, .05
SHELL SECTION, MAT=M1, ELSET=ALL
.1,

Material:

Linear elastic, Young's modulus = 1.0, Poisson's ratio = 0.0.

Boundary conditions:

Node 17 is fully constrained. $ϕ_{z} = $ 0 for all nodes. Nodes 1, 2, and 5 are constrained to move together. Nodes 11, 12, and 15 are constrained to move together.

Loading:

M ${}_{y}=$ −6.0 at node 5. M ${}_{y}=$ 6.0 at node 15.

Results and discussion


Element	Pt.	J	J_elastic	K_I
1	1	4.43 × 10⁶	4.43 × 10⁶	2105.0
1	2	4.43 × 10⁶	4.43 × 10⁶	2105.0
1	3	4.43 × 10⁶	4.43 × 10⁶	2105.0

Input files

exls6bx2.inp: Single-edge notch strip under far-field bending about an axis (along the crack-tip line).

LS3S under far-field tension

Problem description

ELEMENT, TYPE=LS3S, ELSET=ALL
1, 2, 5, 1
SURFACE FLAW, SIDE=POSITIVE
1, .05
5, .05
2, .05
SHELL SECTION, MAT=M1, ELSET=ALL
.1,

Material:

Linear elastic, Young's modulus = 1.0, Poisson's ratio = 0.0.

Boundary conditions:

$u_{x} = u_{y} = $ 0 at nodes 1, 2, and 5.

Loading:

F ${}_{z}=$ 1.0 at nodes 3 and 4. F ${}_{z}=$ 4.0 at node 7.

Results and discussion


Element	Pt.	J	K	J_elastic
1	1	4518.0	67.22	4518.0
1	2	4518.0	67.22	4518.0
1	3	4518.0	67.22	4518.0

Input files

exls3tx2.inp: Single-edge notch strip under far-field tension.

LS6 under Mode I, II, and III loading

Problem description

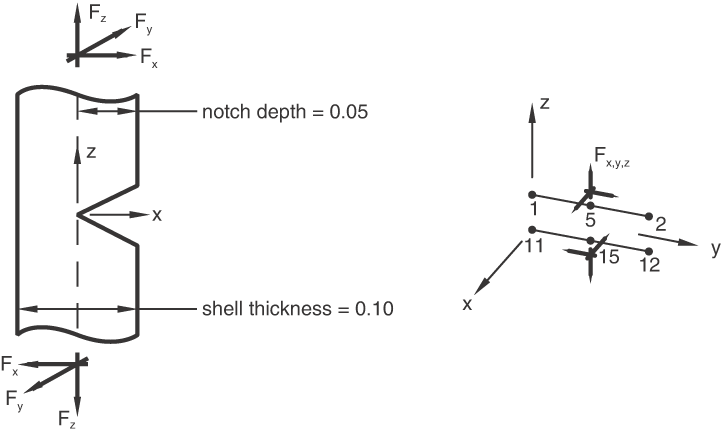
ELEMENT, TYPE=LS6, ELSET=ALL
1, 2, 5, 1, 12, 15, 11
SURFACE FLAW, SIDE=POSITIVE
1, .05
5, .05
2, .05
SHELL SECTION, MAT=M1, ELSET=ALL
.1,

Material:

Linear elastic, Young's modulus = 1.0, Poisson's ratio = 0.0.

Boundary conditions:

Node 17 is fully constrained. $ϕ_{z} = $ 0 for all nodes. Nodes 1, 2, and 5 are constrained to move together. Nodes 11, 12, and 15 are constrained to move together.

Loading:

$F_{x} = F_{y} = F_{z} = $ 1.0 at node 5. $F_{x} = F_{y} = F_{z} = $ −1.0 at node 15.

Results and discussion


Element	Pt.	J	J_elastic	K_I	K_II	K_III
1	1	170.10	170.10	11.20	4.962	−4.472
1	2	170.10	170.10	11.20	4.962	−4.472
1	3	170.10	170.10	11.20	4.962	−4.472

Input files

exls6sx2.inp: Single-edge notch strip under far-field tension (Mode I), in-plane shear (Mode II), and uniform out-of-plane shear (Mode III).