Loading of piezoelectric elements

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

Plane stress and plane strain piezoelectric elements
Three-dimensional piezoelectric elements
Axisymmetric piezoelectric elements

ProductsAbaqus/Standard

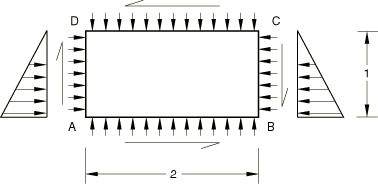
Plane stress and plane strain piezoelectric elements

Elements tested

CPS3E

CPS4E

CPS6E

CPS8E

CPS8RE

CPE3E

CPE4E

CPE6E

CPE8E

CPE8RE

Problem description

Material:

Linear elastic, Young's modulus = 30 × 10⁶, Poisson's ratio = 0.3, no piezoelectric coupling, isotropic dielectric constant 1.0 × 10⁻³.

Boundary conditions:

$u_{x}^{A} = u_{y}^{A} = φ^{A} = $ 0, $u_{y}^{B} = φ^{B} = $ 0.

Loading:

Distributed pressure of 1000/length on each edge.

Equivalent concentrated shear forces corresponding to distributed shear loading of 1000/length on each edge in the directions shown.

Distributed charges of 1000/length on each edge.

Concentrated charges at each node to negate the distributed charges, except for the distributed charge of 1000/length on the top surface.

Reference solution

Stresses

Both plane stress and plane strain elements,

$σ_{x x} = σ_{y y} = σ_{x y} = $ −1000;

and for plane strain elements,

$σ_{z z} = $ −600.

Strains

Plane strain elements,

$ε_{x x} = ε_{y y} = $ −1.7333 × 10⁻⁵, $γ_{x y} = $ −8.6667 × 10⁻⁵.

Plane stress elements,

$ε_{x x} = ε_{y y} = $ −2.3333 × 10⁻⁵, $γ_{x y} = $ −8.6667 × 10⁻⁵.

Electrical fluxes

Both plane stress and plane strain elements, $q_{x x} = $ 0, $q_{y y} = $ −1000.

Electrical potential gradients

Both plane stress and plane strain elements, $E_{x x} = $ 0, $E_{y y} = $ −1.0 × 10⁶.

Displacements

$u_{x} = x ε_{x x} + y γ_{x y}$ , $u_{y} = y ε_{y y}$ .

Potentials

$φ = - y E_{y y}$ .

Results and discussion

Elements using reduced integration may have additional boundary conditions to those specified above. All elements yield exact solutions.

Section output requests to the results (.fil) file and to the data (.dat) file are used in some of the input files to output accumulated quantities on the face in the x–y plane.

Input files

ecs3efs1.inp: CPS3E elements.
ecs4efs1.inp: CPS4E elements.
ecs6efs1.inp: CPS6E elements.
ecs8efs1.inp: CPS8E elements.
ecs8ers1.inp: CPS8RE elements.
ece3efs1.inp: CPE3E elements.
ece4efs1.inp: CPE4E elements.
ece6efs1.inp: CPE6E elements.
ece8efs1.inp: CPE8E elements.
ece8ers1.inp: CPE8RE elements.

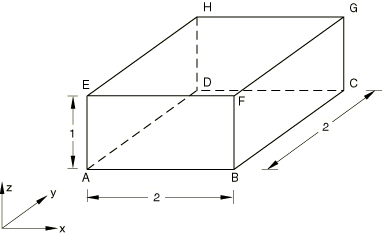
Three-dimensional piezoelectric elements

Elements tested

C3D4E

C3D6E

C3D8E

C3D10E

C3D15E

C3D20E

C3D20RE

Problem description

Material:

Linear elastic, Young's modulus 30 × 10⁶, Poisson's ratio 0.3, no piezoelectric coupling, isotropic dielectric constant 1.0 × 10⁻³.

Boundary conditions:

$u_{x}^{A} = u_{y}^{A} = u_{z}^{A} = φ^{A} = 0$ , $u_{y}^{B} = φ^{B} = 0$ , $φ^{C} = 0$ , $u_{z}^{D} = φ^{D} = 0$ , $u_{x}^{E} = 0$ .

Loading:

Distributed pressure of 1000/area on each face, and equivalent concentrated forces for shear loading, defined such that all three shear stresses are of magnitude −1000.

Distributed charges of 1000/area on each face.

Concentrated charges at each node to negate the distributed charges, except for the distributed charge of 1000/area on the top surface.

Reference solution

Stresses: $σ_{x x} = σ_{y y} = σ_{x y} = σ_{x y} = σ_{x z} = σ_{y z} = $ −1000.
Strains: $ε_{x x} = ε_{y y} = ε_{z z} = $ −1.3333 × 10⁻⁵, $γ_{x y} = γ_{y z} = γ_{x z} = $ −8.6667 × 10⁻⁵.
Electrical fluxes: $q_{x x} = $ 0, $q_{y y} = $ 0, $q_{z z} = $ −1000.
Electrical potential gradients: $E_{x x} = $ 0, $E_{y y} = $ 0, $E_{z z} = $ −1.0 × 10⁶.
Displacements: $u_{x} = x ε_{x x} + y γ_{x y}, u_{y} = y ε_{y y} + z γ_{y z}, u_{z} = z ε_{z z} + x γ_{x z}$ .
Potentials: $φ = - z E_{z z}$ .

Results and discussion

Elements using reduced integration may have additional boundary conditions to those specified above. All elements yield exact solutions.

Section output requests to the results (.fil) file and to the data (.dat) file are used in some of the input files to output accumulated quantities on the face in the x–y plane.

Input files

ec34efs2.inp: C3D4E elements.
ec36efs2.inp: C3D6E elements.
ec38efs2.inp: C3D8E elements.
ec3aefs2.inp: C3D10E elements.
ec3fefs2.inp: C3D15E elements.
ec3kefs2.inp: C3D20E elements.
ec3kers2.inp: C3D20RE elements.

Axisymmetric piezoelectric elements

Elements tested

CAX3E

CAX4E

CAX6E

CAX8E

CAX8RE

Problem description

Material:

Linear elastic, Young's modulus 30 × 10⁶, Poisson's ratio 0.3, no piezoelectric coupling, isotropic dielectric constant 1.0 × 10⁻³.

Boundary conditions:

$u_{z}^{A} = u_{z}^{B} = φ^{A} = φ^{B} = 0$ .

Loading:

Distributed pressure of 1000/area on each face.

Distributed charges of 1000/area on each face.

Concentrated charges at each node to negate the distributed charges, except for the distributed charge of 1000/area on the top surface.

Reference solution

Stresses: $σ_{r r} = σ_{θ θ} = σ_{z z} = $ −1000, $σ_{r z} = $ 0.
Strains: $ε_{r r} = ε_{θ θ} = ε_{z z} = $ −1.3333 × 10⁻⁵, $ε_{r z} = $ 0.
Electrical fluxes: $q_{r r} = $ 0, $q_{z z} = $ −1000.
Electrical potential gradients: $E_{r r} = $ 0, $E_{z z} = $ −1.0 × 10⁶.
Displacements: $u_{r}$ = −1.33 × 10⁻² along $r = $ 1000, $u_{z} = $ −1.33 × 10⁻⁵z.
Potentials: $φ = - z E_{z z}$ .

Results and discussion

Elements using reduced integration may have additional boundary conditions to those specified above. All elements yield exact solutions.

Section output requests to the results (.fil) file and to the data (.dat) file are used in some of the input files to output accumulated quantities on the face in the x–y plane.

Input files

eca3efs3.inp: CAX3E elements.
eca4efs3.inp: CAX4E elements.
eca6efs3.inp: CAX6E elements.
eca8efs3.inp: CAX8E elements.
eca8ers3.inp: CAX8RE elements.