Gumbel Distribution

The Gumbel probability density function for the largest element is as follows:

f_{X} (x) = β \exp [- β (x - α) - \exp [- β (x - α)]] - \infty \leq x \leq \infty, β > 0

The Gumbel probability density function for the smallest element is similarly:

f_{X} (x) = β \exp [β (x - α) - \exp [β (x - α)]] - \infty \leq x \leq \infty, β > 0

In both cases the parameter $α$ is a measure of location and $β$ is a measure of dispersion.

The Gumbel distribution function for the largest element is as follows:

F_{X} (x) = \exp {- \exp [- β (x - α)]} - \infty \leq x \leq \infty, α > 0

The Gumbel distribution function for the smallest element is similarly:

F_{X} (x) = 1 - \exp [β (x - α)] - \infty \leq x \leq \infty, α > 0

The mean value and standard deviation of the random variable $X$ for the Gumbel distribution for the largest element is as follows:

μ_{X} = α + \frac{γ}{β} \approx α + \frac{0.5772}{β} .

The mean value and standard deviation of the random variable $X$ for the Gumbel distribution for the smallest element is similarly:

μ_{X} = α + \frac{γ}{β} \approx α - \frac{0.5772}{β}

and

σ_{X} = \frac{π}{\sqrt{6} β} .

where $γ \approx 0.5772$ is Euler’s constant.

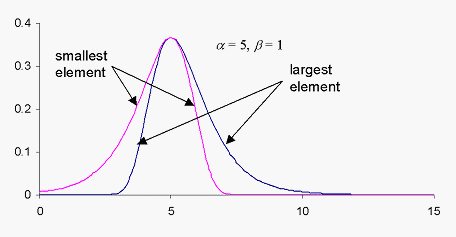
The Gumbel probability density function, as shown in the figure below, is often used to describe the breaking strength of materials, breakdown voltage in capacitors, and gust velocities encountered by an aircraft.