Triangular Distribution

In triangular distribution the three parameters are:

a lower limit location parameter, $a$ ,
an upper limit location parameter, $b$ , and
a shape parameter that defines the mode or peak of the triangle, $c$ .

The triangular probability density function for a random variable $X$ is:

$\begin{array}{l} f_{X} (x) & = 2 (x - a) / [(b - a) (c - a)] & a \leq x \leq c \\ = 2 (b - x) / [(b - a) (b - c)] & c \leq x \leq b \\ = 0 & otherwise \end{array}$

The triangular distribution function is:

$\begin{array}{l} F_{X} (x) & = \frac{{(x - a)}^{2}}{(b - a) (c - a)} & a \leq x \leq c \\ = 1 - \frac{{(b - x)}^{2}}{(b - a) (b - c)} & c \leq x \leq b \end{array}$

The mean value and standard deviation of the random variable $X$ for the exponential distribution are given by

$μ_{X} = \frac{a + b + c}{3}$

and

$σ_{X} = \sqrt{\frac{a^{2} + b^{2} + c^{2} - a b - a c - b c}{18}} .$

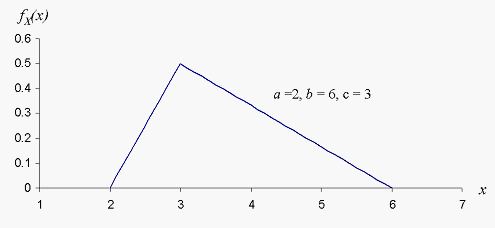
The triangular probability density function, as shown in the figure below, is commonly used when the actual distribution of a random variable is not known but three pieces of information are available:

a lower limit that the random variable will not go below,
an upper limit that the random variable will not exceed, and
a “most likely” (expected peak) value.