Uniform Distribution

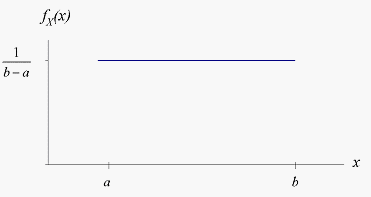
The uniform probability density function is given by

\begin{array}{l} f_{X} (x) & = \frac{1}{b - a} & a \leq x \leq b \\ = 0 & otherwise \end{array}

where the parameters $a$ and $b$ define the range of the uniform distribution. The uniform distribution function is

F_{X} (x) = \frac{x - a}{b - a} a \leq x \leq b .

The mean value and standard deviation of the random variable $X$ for the uniform distribution are given by

μ_{X} = \frac{a + b}{2}

and

σ_{X} = \frac{b - a}{2 \sqrt{3}} .

The uniform probability density function, as shown in the figure below, is used when only a range of possible values for a random variable is known.