Conditions for Linear Analysis | ||
| ||
For a linear analysis to be valid, the following assumptions must be true:
-
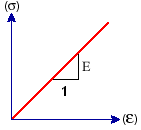
All materials in the model exhibit linear elastic behavior; that is, stresses are linearly proportional to strains (Hooke's law). If the load is removed, the geometry returns to its original shape with no permanent deformation.
- Deformations are small in relation to the dimensions of the model.
- All loads are applied slowly and gradually until they reach their full magnitudes. After reaching their full magnitudes, loads remain constant in magnitude and direction.Note: This assumption allows us to neglect inertial and damping forces due to negligibly small accelerations and velocities. Time-variant loads that induce considerable inertial and damping forces may warrant dynamic analysis. Dynamic loads (such as earthquake, oscillatory, impact, or shock loads) change with time and in many cases induce considerable inertial and damping forces that cannot be neglected.
- Boundary conditions do not vary during the application of loads. The loads do not cause changes in contact conditions between parts.
In a linear analysis there is a linear relationship between the applied loads and the induced response of the system. For example, if a linear spring extends statically by 1 m under a load of 10 N, it will extend by 2 m when a load of 20 N is applied.
This means that in a linear analysis the flexibility of the structure need only be calculated once (by assembling the stiffness matrix and inverting it). The linear response of the structure to other load cases can be found by multiplying the new vector of loads by the inverted stiffness matrix (or flexibility matrix).
In addition, the structure's response to various load cases can be scaled by constants to determine its response to a completely new load case, provided that the new load case is the sum (or multiple) of previous ones. This principle of superposition of load cases assumes that the same boundary conditions are used for all the load cases.
A linear static solution is not valid if any of these points are violated. The relationship between the applied loads (generalized force) and the response (generalized displacement) becomes nonlinear, and a nonlinear analysis must be performed to get accurate results that reflect the true behavior of the model.
A graphical representation of the analysis type based on the generalized force/displacement relationship is shown below.
