This method is appropriate for cases where the loading is proportional; that is, where the
load magnitudes are governed by a single scalar parameter. The method can provide solutions
even in cases of complex, unstable response such as that shown in the following figure:
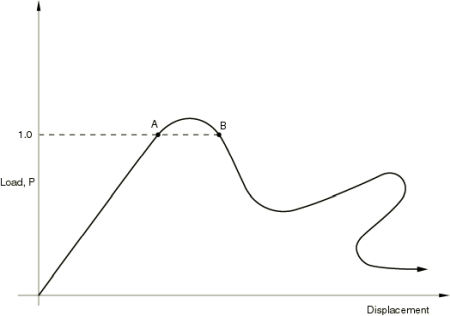
The Riks method uses the load magnitude as an additional unknown; it solves simultaneously
for loads and displacements. Therefore, the solver requires another quantity to measure the
progress of the solution. Abaqus/Standard uses the “arc length” along the static equilibrium path in load-displacement space. This
approach provides solutions regardless of whether the response is stable or unstable.
You can define a stop condition for a static Riks analysis by specifying a maximum load
proportionality factor, a maximum displacement at a node, or both. The solver ends the
analysis if the computed solution crosses either of these limits. If the solution does not
exceed one of these limits, the analysis ends after executing the maximum number of increments
for the step.
