About Aligning

This operation is useful with mechanical shapes, where canonic shapes can be defined. When such shapes can be used, this method is quicker than the other proposed types.

You need to recognize canonic shapes:

• On the cloud to align, for example, with Digitized Shape to Surface
• Then on the reference (by extracting faces or creating points, lines and planes representing fixed constraints).

These canonic shapes are not necessarily the same (any association of points/lines/planes is possible).

Then match the canonic shapes by pair, one on the cloud to align, the other on the reference. You can match one constraint element of the cloud to align with several constraint elements (whatever their type) of the reference, or vice versa (a plane can be matched with three different points in three different constraints, for example).

Be careful to have consistent constraints, regarding the geometry. For example:

• Do not match three points with two different planes.
• If you match two normals to planes, be careful that they have the same orientation.
• When you select a cylinder or a circle, the constraint element taken into account is their center axis, that is, a line.
• When you select a sphere, the constraint element taken into account is its center point.
• Even if overconstraints are accepted, the constraints should form an isostatic system:
  • A 3D object has 6 degrees of freedom, that is, 3 translations and 3 rotations.
  • Creating an isostatic system means that the 3 translations and the 3 rotations are locked.
  • Below are the degrees of freedom locked by each pair of constraints:

    	point	line	plane
    point	3 translations	2 translations	1 translation
    line	2 translations	2 translations and 2 rotations	1 translation and 1 rotation
    plane	1 translation	1 translation and 1 rotation	1 translation and 2 rotations

In a general case, you should combine the constraints to lock all the degrees of freedom.

Statistics give you useful information.

You can retrieve the history of the computations and revert to a given combination of constraints before creating the aligned model.

You can see if a constraint with a strict priority is fully respected, and to which extend the other constraints are respected.

You can find the distance gaps for constraints of the types point/point, point/line, point/plane, line/line, line/plane and plane/plane, as well as the angular gaps for constraints of the types line/line, line/plane and plane/plane. Since those gaps are computed from the infinite support of lines and planes that make the constraints, the distance between two non parallel planes (or a line and a plane) is null. Only significant gaps between a line and a plane or between two planes are displayed (that is, only when the two constraint elements are parallel).

The statistics are given for the constraint elements. They do not refer to the real gaps between the cloud to align and the reference.

A constraint with a Strict priority is not fully respected when the distance is greater than 0.001 or the angle is greater than 0.5. This may happen when a constraint with a Strict priority is applied simultaneously to other constraints.

If the constraints are not consistent, an information message is displayed. You can then decide whether the result is satisfactory or not.

Similarly to alignment with constraints, RPS alignment is defined by a set of constraints but there are some differences between these two alignment commands.

Align with RPS	Align with Constraints
A well-defined RPS alignment must always be isostatic, to ensure the repeatability of alignment conditions.	Non-isostatic system is accepted.
Constraints are defined only by points, circles, and arcs.	Constraints can also be defined by planes, cylinders, and spheres.
When a circle or an arc is input, its center position, that is, a point, is taken into account.	When a circle or an arc is input, its center axis, that is, a line, is taken into account.
Only translations can be frozen.	Translations and rotations can be frozen.
For each RPS constraint, at least one axis must be frozen.	-
In a point - point constraint, you can freeze one, two, or three axes of the point on the reference.	In a point - point constraint, all the three axes (X, Y, and Z) of the point on the reference are automatically frozen.

The constraints in an RPS alignment must comply with some rules.

Since a RPS alignment is isostatic, the following conditions must be satisfied:

• In a first axis, three RPS constraints must be frozen to define a plane.
• In a second axis, two RPS constraints must be frozen to define a line.
• In a third axis, one RPS constraint must be frozen to define the locating point.

Defining a RPS alignment requires a minimum of 3 RPS constraints and a maximum of 6 RPS constraints. In some situations, Aligning with RPS leads to multiple solutions that are often symmetrical and the solution proposed by the command may be different from the one you expect. This happens particularly if the reference is too far away or too rotated from the cloud to align.

Tips: The light is yellow when there are too few or too many constraints to define the RPS alignment, that is, the alignment is not fully defined. The light is green when the RPS alignment is fully defined and the alignment result is isostatic. The light is red when the RPS alignment is fully defined but the alignment result is not isostatic.

Some tips make the selection of spheres easier.

Pick the sphere in a direction orthogonal to the part to process, that is, along the green axis and not along the black axis in our example:

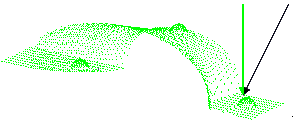
For an easier sphere recognition, pick in the middle of the sphere, not at the edge.

If you use 3 spheres, they should not form an isosceles nor an equilateral triangle (the system could not find out the right solution between the two or six possible solutions).

If you know the radius of the spheres, select the Constrained check box and enter the radius to compute the spheres.

If you do not know the radius of the spheres, click the first sphere. The app computes the radius and updates the input accordingly. Then select the Constrained check box and select other spheres: they have now the same radius.