The one-dimensional cavitation problem

This example illustrates the use of Abaqus/Explicit to model a one-dimensional cavitation problem. A fluid column supporting a floating mass-spring system is studied, and the results obtained using Abaqus/Explicit are compared with those obtained by Bleich and Sandler (1970) and Sprague and Geers (2001).

This page discusses:

Problem description
Results and discussion
Input files
References
Figures

ProductsAbaqus/Explicit

When an underwater explosion occurs, a compressive wave is generated. If the wave reaches the free surface of the water, the reflected wave is dilational, causing tensile stress in the water. Water cannot sustain a high value of tension and can disassociate, creating a region of cavitation that has a substantial influence on the response of marine structures. In this example the ability of Abaqus/Explicit to model this situation accurately is illustrated using a one-dimensional problem.

Problem description

A one-dimensional fluid column in a rigid pipe with a constant cross-sectional area is modeled with AC2D4R elements. At the top of the column the fluid is coupled to an idealized floating structure, represented by two vertically oriented masses ( $M_{1}$ and $M_{2}$ ) connected by a spring with stiffness K. Figure 1 shows a schematic of the model. The fluid-solid system is excited by a plane, upward-propagating, step-exponential wave, applied at the bottom of the fluid column. A plane wave absorbing boundary is also applied at the bottom of the column, which is exact for one-dimensional acoustic waves.

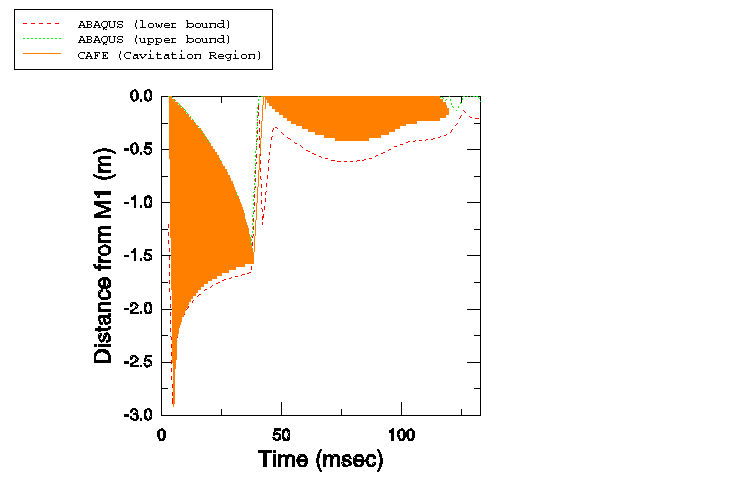
To simulate the mass $M_{1}$ , one point mass element is attached to a node vertically aligned with each of the uppermost two nodes of the fluid column. In the mass-spring models two other point masses are attached to nodes 5.08 m above the uppermost fluid nodes to simulate the mass $M_{2}$ , and the corresponding point mass nodes are linked with spring elements. At the top of the fluid column, the fluid response is coupled to that of the structure using a tie constraint. At the bottom of the fluid column, a plane wave, nonreflecting boundary condition is applied. The step-exponential wave is applied on the bottom surface of the fluid column using incident wave loading, which refers to an amplitude curve that contains the discretized pressure-time history of the wave at the standoff point (the bottom of the fluid column). The point masses are constrained in all directions except the vertical (degree of freedom 2). The nondefault total wave formulation is used to capture the effects of cavitation. The cavitation pressure limit for the acoustic medium is set to zero, thus initiating cavitation whenever the absolute pressure (sum of the incident, scattered, and static pressure) becomes negative. The initial acoustic static pressure in the fluid is specified.

Single-mass case

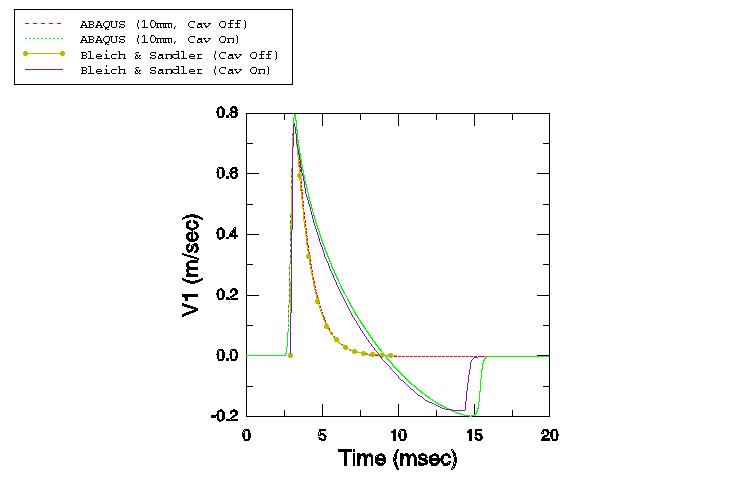
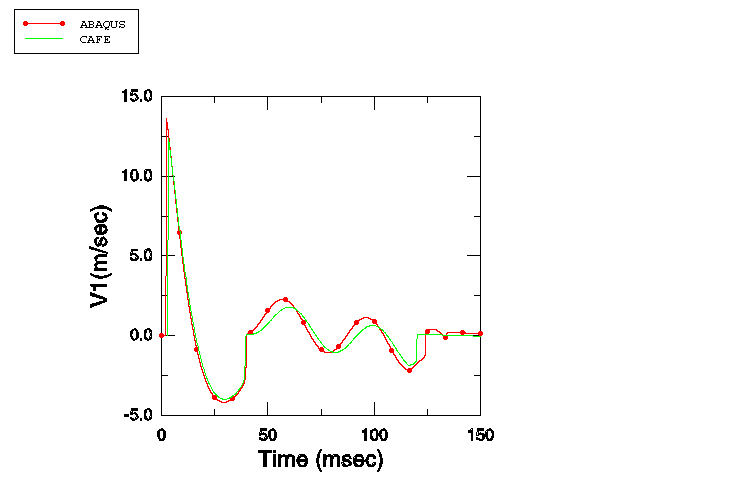
In the first part of this example $M_{2}$ is set to zero, duplicating the model problem published in Bleich and Sandler (1970).

The fluid column depth is 3.81 m. A single stack of AC2D4R elements is used to mesh this column, with all elements 38.1 mm in width and 1.0 m in out-of-plane thickness. The draft of the floating mass is 0.145 m. Atmospheric pressure is 0.101 MPa. The fluid density is 989.0 kg/m³, the acoustic velocity is 1451.0 m/s, and the acceleration of gravity is 9.81 m/s². The fluid properties yield a bulk modulus of 2.082242 GPa, which is the value that is specified along with the fluid density. The initial conditions are specified in such a manner that the pressure at the free surface is the sum of the atmospheric pressure and the pressure caused by the floating mass. Hence, the initial pressure is applied as a linear variation from p = $P_{a t m}$ = 0.101 MPa at a height of 0.145 m (to include the effect of the floating mass) to p = $P_{a t m} + ρ_{f} (g) (d e p t h)$ = 0.13937177 MPa at the bottom of the fluid column. The maximum pressure in the step-exponential wave is 0.7106 MPa, and the decay time is 0.9958 ms. This model is studied using a coarse mesh of 100 elements, each 38.1 mm in height, and a fine mesh of 381 elements, each 10 mm in height.

In addition, two time increment sizing methods are compared: that used by Sprague and Geers, and the time increment size automatically computed by Abaqus/Explicit. Sprague and Geers have used a fixed time increment $Δ t$ = $Δ t_{c f l}$ /2, where $Δ t_{c f l}$ is the Courant-Friedrichs-Lewy time increment limit, computed as $Δ t_{c f l}$ = $Δ x$ /c, where $Δ x$ is the element height. Thus, for the 38.1 mm case this requirement yields a time increment of 13.12887 $μ$ s, while for the 10 mm case it yields a time increment of 3.445889 $μ$ s.

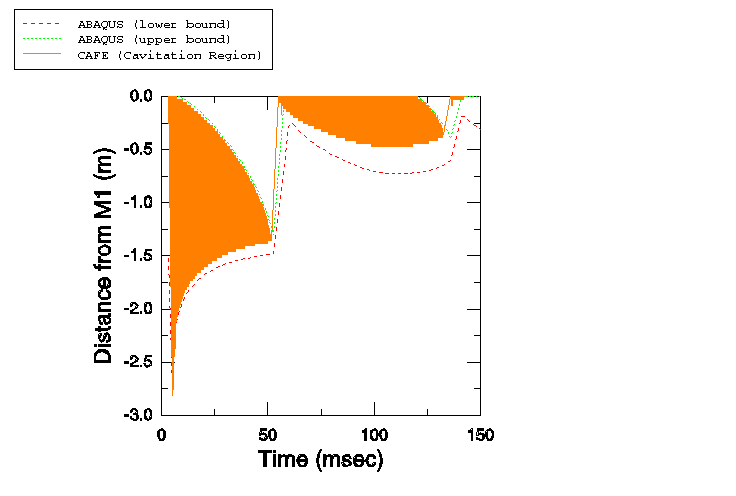
Multiple-mass case

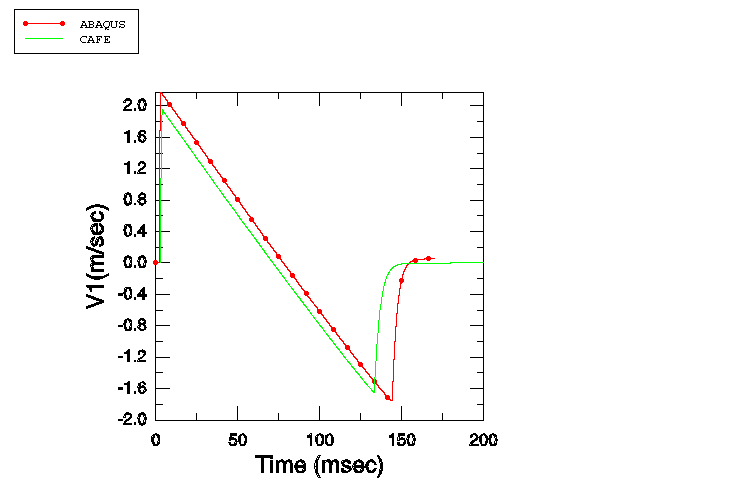
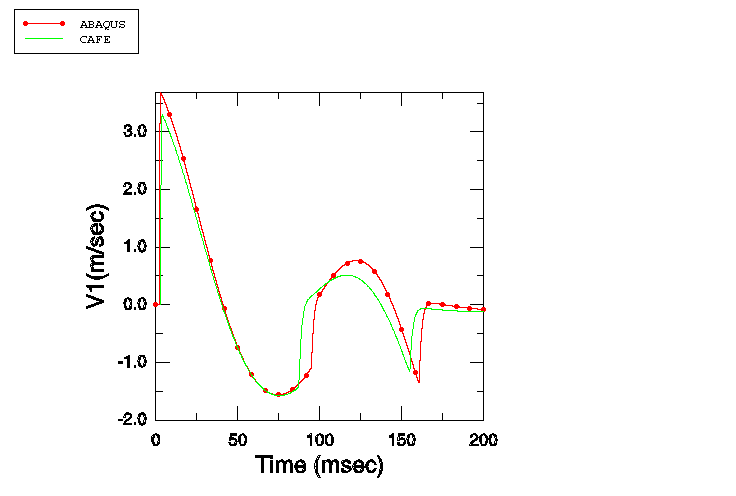
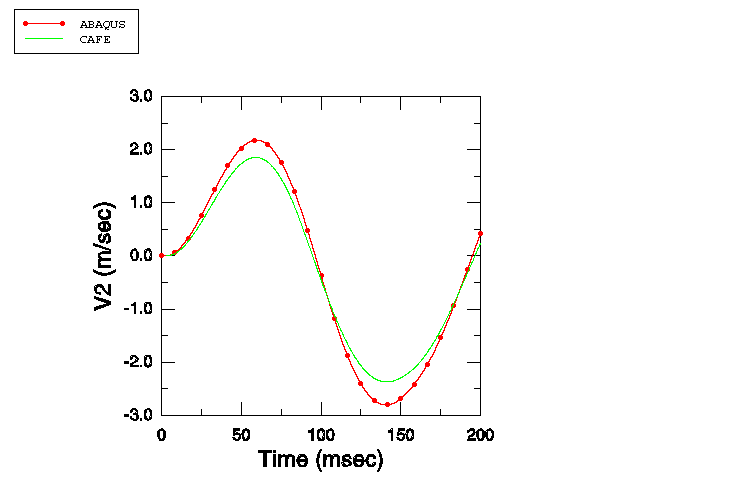
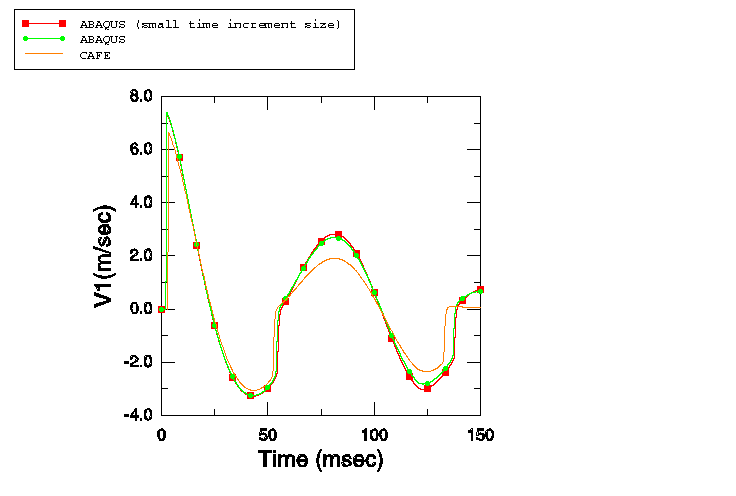
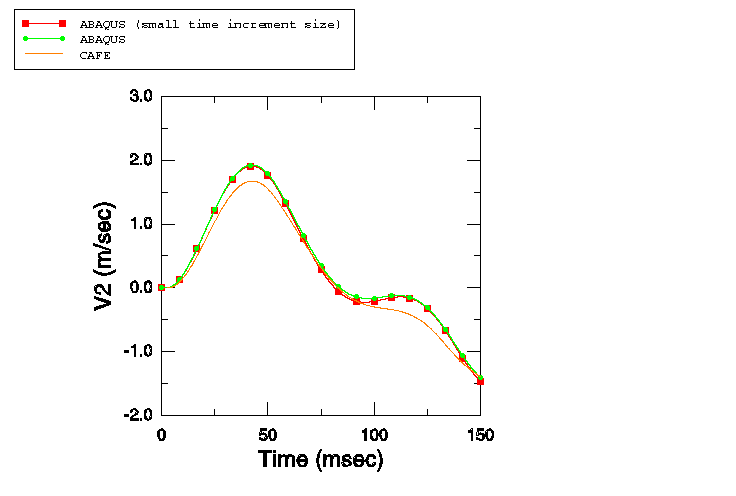
In the second part of this example the ratio of $M_{2}$ / $M_{1}$ is varied to study the cases of Sprague and Geers (2001). Four cases are examined: $M_{2}$ / $M_{1}$ = 0, $M_{2}$ / $M_{1}$ = 1, $M_{2}$ / $M_{1}$ = 5, and $M_{2}$ / $M_{1}$ = 25. The results obtained are compared with those obtained by Sprague and Geers (2001) with Cavitating Acoustic Finite Element (CAFE) models.

The fluid column depth is 3.0 m. A single stack of AC2D4R elements is used to mesh this column, with all elements 2.5 mm in height, 10 mm in width, and 1.0 m in out-of-plane thickness. Atmospheric pressure is 0.101 MPa. The fluid density is 1025.0 kg/m³, the speed of sound is 1500.0 m/s, and the acceleration of gravity is 9.81 m/s². The draft is 5.08 m for all the models, so that the mass of displaced fluid is equal to the displaced volume times the fluid mass density, or 52.07 kg. In the case where $M_{2}$ / $M_{1}$ = 0, this mass is entirely assigned to $M_{1}$ . In the second case $M_{2}$ / $M_{1}$ = 1. To keep the draft constant at 5.08 m, the total mass of $M_{1}$ and $M_{2}$ must equal 52.07 kg. Dividing it equally between $M_{1}$ and $M_{2}$ yields $M_{1}$ = $M_{2}$ = 26.035 kg. For the case $M_{2}$ / $M_{1}$ = 5, $M_{1}$ is assigned a mass of 8.678333 kg, while $M_{2}$ is assigned a mass of 43.391667 kg. For the fourth case $M_{2}$ / $M_{1}$ = 25; hence, $M_{1}$ is 2.0026923 kg, while $M_{2}$ is 50.067308 kg.

The spring constants defined in the reference paper are such that the fixed-base natural frequency of mass $M_{2}$ is 5 Hz in all the cases: K = (5 × 2 $π$ ) $^{2}$ $M_{2}$ . Thus, for the case $M_{2}$ / $M_{1}$ = 1, K = 12847.758 kg/s²; for $M_{2}$ / $M_{1}$ = 5, K = 21412.929 kg/s²; and for $M_{2}$ / $M_{1}$ = 25, K = 24707.226 kg/s².

The initial conditions are specified as in the single-mass case, with atmospheric pressure of 0.101 MPa applied 5.08 m above the free surface and 0.212412 MPa applied at a depth of 6 m. The maximum pressure in the step-exponential wave is 16.15 MPa, and the decay time is 0.423 ms.

For all the mass ratio cases, analyses are performed using a fixed time increment size $Δ t$ = $Δ t_{c f l}$ /2, which is 0.8333 $μ$ s. For the case where $M_{2}$ / $M_{1}$ = 5, the effect of using a smaller time increment size ( $Δ t$ = $Δ t_{c f l}$ /20 = 0.08333 $μ$ s) while holding all other parameters constant is also analyzed.

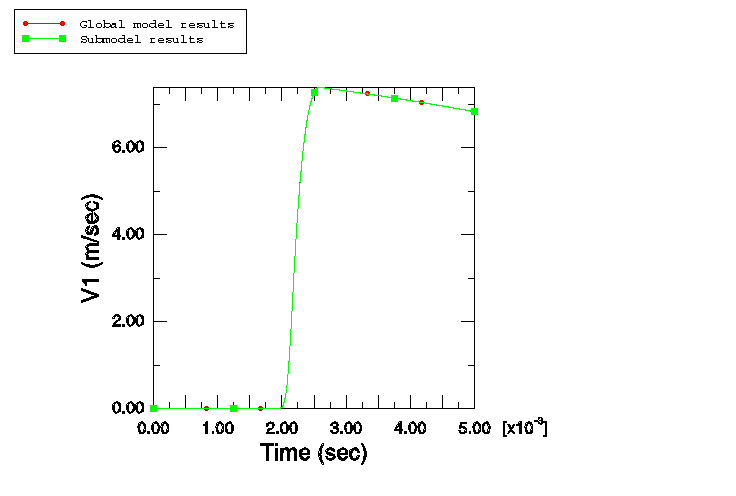
Submodeling

These types of analyses can also be performed using the acoustic-to-structure submodeling technique; this study includes a case where the results obtained by performing an analysis with the submodeling technique are compared with those obtained using the default global analysis technique. The submodeling technique illustrated here is useful in situations where the structural response is of primary interest and the presence of the fluid is required mainly for the application of the underwater explosive load onto the structure. In such situations it is possible to perform a single global analysis with a fluid mesh, followed by multiple submodel analyses without the fluid mesh wherein the structural parameters are varied and the effects analyzed. Due to the absence of the fluid mesh in the submodel analyses, computational effort may be significantly reduced. In this study the submodeling technique is illustrated for the case $M_{2}$ / $M_{1}$ = 5 and is run for a step time of 5 ms. First, a global analysis is performed and the structural displacements (U) and acoustic pressures (POR) at the top of the fluid stack are written to the results file. Following the completion of the global analysis, the submodel analysis is performed, wherein the model consists of the structure only and no fluid mesh is present. This structural submodel is driven by the acoustic pressure results extracted from the global analysis.

Modeling cavitation using displacement-based elements

In certain underwater explosion situations—for example, when an underwater explosion occurs near a submarine—the explosion can cause large structural displacements of the submarine hull. In cases where the structural displacements are extremely large, as occurs during plastic failure of the hull, the fluid migrates to fill the displaced volume. This large motion of the fluid is best modeled with displacement-based continuum elements that can be adaptively meshed to avoid extreme mesh distortions in Abaqus/Explicit. To demonstrate this modeling technique, the cavitation of the one-dimensional fluid column is modeled using a single stack of CPE4R elements instead of AC2D4R elements. The geometry and material properties used are identical to the multiple-mass case. The effect of the hydrostatic pressure is simulated using gravity loading on the fluid column, with an additional distributed pressure load defined on the top of the fluid column to account for the effect of the atmospheric pressure and the draft of the floating masses. To establish an initial equilibrated state, geostatic initial stresses are specified. An equation-of-state material of the linear $U_{s} - U_{p}$ form is used to model the fluid, and a tensile failure model is used to simulate cavitation in the fluid medium. The material parameters are chosen to closely match the acoustic medium properties used for the acoustic element simulation. At the bottom of the fluid column, nonreflecting boundary conditions are applied by defining a displacement-based infinite element of type CINPE4. Adaptive meshing is used to adaptively remesh the fluid domain to prevent excessive mesh distortions. The loading is identical to that used for the multiple-mass case.

Results and discussion

The results are analyzed by comparing the predictions made by running double precision Abaqus/Explicit to those in the referenced literature.

Single-mass case

We compare the upward velocity of mass $M_{1}$ and the spatiotemporal variation of the cavitated region in the fluid obtained using Abaqus/Explicit to those same quantities obtained by Bleich and Sandler. Figure 2 shows the results obtained by Abaqus/Explicit plotted alongside those obtained analytically by Bleich and Sandler for the coarse mesh consisting of 38.1 mm elements. Figure 3 shows the comparison for the finer mesh consisting of 10 mm elements, while Figure 4 shows the comparisons of the cavitation region. The results obtained by Abaqus/Explicit show good comparison with the theoretical results. It is also found that the difference in results between using a predetermined fixed time increment size and the automatic time incrementation scheme in Abaqus/Explicit is insignificant.

Multiple-mass case

Figure 5 through Figure 11 show the Abaqus/Explicit results alongside those calculated numerically by Sprague and Geers. We compare velocities $v_{1}$ and $v_{2}$ and the cavitated region. There is good comparison in all cases. In the $M_{2}$ / $M_{1}$ = 5 case the velocity obtained by using a reduced time increment size is also shown. There is no significant effect of reducing the time increment size in Abaqus/Explicit on the velocities $v_{1}$ and $v_{2}$ . Figure 12 through Figure 16 show the cavitation region comparisons for the four different mass ratios. Comparing Figure 14 and Figure 16, we see that the cavitation region computed by Abaqus/Explicit shows a dependence on the time increment size, which is in agreement with the findings of Sprague and Geers.

Submodeling

Figure 17 and Figure 18 show the comparisons between the results obtained from the global analysis and those obtained from the submodel analysis for the $M_{2}$ / $M_{1}$ = 5 case. As can be seen, the results are identical.

Modeling cavitation using displacement-based elements

Figure 19 and Figure 20 show the comparisons between the results obtained from the multiple-mass case analysis using acoustic elements and those obtained using displacement-based elements. The results are shown for a mass ratio $M_{2}$ / $M_{1}$ = 5. The results from the two analyses are seen to be in good agreement.

Input files

1_mass_coarse.inp: Bleich and Sandler model, coarse mesh.
1_mass_fine.inp: Bleich and Sandler model, fine mesh.
2_mass_0_1.inp: $M_{2}$ / $M_{1}$ = 0.
2_mass_1_1.inp: $M_{2}$ / $M_{1}$ = 1.
2_mass_5_1.inp: $M_{2}$ / $M_{1}$ = 5.
2_mass_25_1.inp: $M_{2}$ / $M_{1}$ = 25.
2_mass_5_1_global.inp: $M_{2}$ / $M_{1}$ = 5, global model.
2_mass_5_1_sub.inp: $M_{2}$ / $M_{1}$ = 5, submodel.
2_mass_5_1_displbased.inp: $M_{2}$ / $M_{1}$ = 5, displacement-based elements.

References

Bleich, H. H., and I. S. Sandler, “Interaction between Structures and Bilinear Fluids,” International Journal of Solids and Structures, vol. 6, pp. 617–639, 1970.
Sprague, M. A., and T. L. Geers, “Computational Treatments of Cavitation Effects in Near-Free-Surface Underwater Shock Analysis,” 72nd Shock and Vibration Symposium Proceedings, 2001.

Figures