Dynamic response of a two degree of freedom system

This example verifies the use of nonlinear springs and direct, implicit, dynamic integration in a simple example for which an independent solution is available (Underwood and Park, 1981).

This page discusses:

ProductsAbaqus/Standard

Problem description

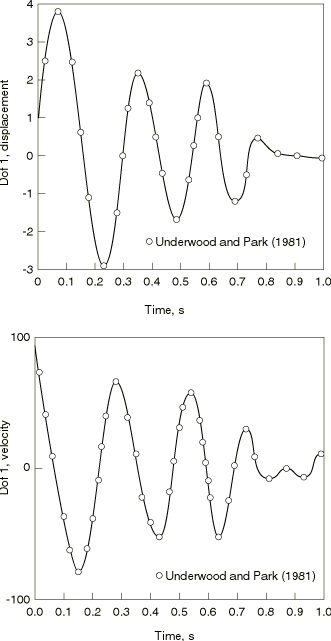
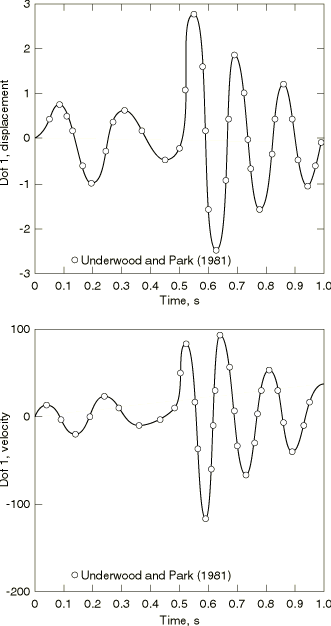
The system consists of two nonlinear springs, each connecting a mass to a fixed point, with a linear spring and a dashpot between the masses. The system is shown in Figure 1. The spring characteristics, the initial conditions, and the forcing functions are also shown in the figure. All values are assumed to be in consistent units.

For direct comparison with the solution of Underwood and Park (1981), the analysis is run with fixed time increments. In Underwood and Park (1981) a time increment of 0.0005 is shown to be very accurate with the central difference (explicit) integration operator, while a time increment of 0.03 is less accurate. In this study the time increment chosen is 0.01. This gives results that agree closely with those reported by Underwood and Park (1981).

Results and discussion

The displacement and velocity histories of the two masses are shown in Figure 2 and Figure 3. The results obtained by Underwood and Park (1981) are shown in the same figures. The agreement is quite close.

Input files

2dofdynamics.inp

Dynamic analysis.

2dofdynamics_depend.inp

Identical to the input data shown in 2dofdynamics.inp, except that temperature- and field-variable-dependent spring and dashpot properties are used.

References

  1. Underwood,  P.,  and K. C. Park, “STIND/CD: A Stand-Alone Explicit Time Integration Package for Structural Dynamic Analysis,” International Journal for Numerical Methods in Engineering, vol. 17, pp. 1285–1312, 1981.

Figures

Figure 1. Two degree of freedom nonlinear spring-mass system.

Figure 2. Displacement and velocity histories of left-hand mass.

Figure 3. Displacement and velocity histories of right-hand mass.