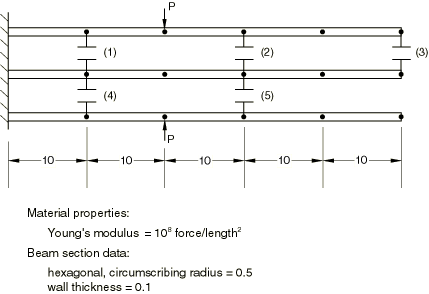
Problem description
Each cantilever is modeled using five cubic beam elements of type B23. Initially all gaps are open, with an initial gap clearance of 0.01. The pinching loads are increased monotonically from 0 to 200. The beam lengths, modulus, and cross-section are shown in Figure 1. (The units of dimension and force are consistent but not physical.)
The loads are applied in 10 equal increments, with the increment size given directly in the static analysis.