The results for each test are presented in two plots: one showing the
stress/strain response and the other showing the variation of the permanent
volumetric strain with the applied stress. For each plot two sets of data are
presented: one corresponds to Coffin's experimental data, and the other
corresponds to the
Abaqus
simulation.
Figure 2,
Figure 3,
and
Figure 4
compare the prediction of the model with the experimental test data in uniaxial
tension and uniaxial compression, respectively. All the figures show good
agreement between the test data and experimental results. This behavior is to
be expected since the model is calibrated using uniaxial test data.
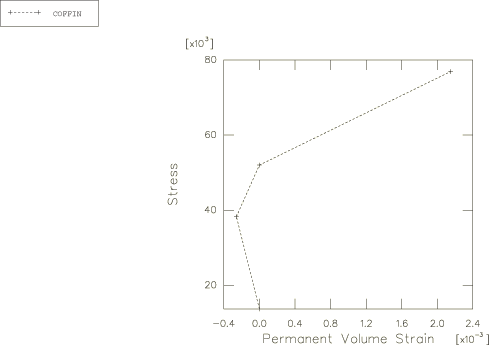
Figure 5
shows that small (compared to the strain in
Figure 4)
permanent volume changes were observed in the uniaxial compression experiment.
The model in
Abaqus
predicts zero permanent volume change under uniaxial compression and higher
confining stresses.
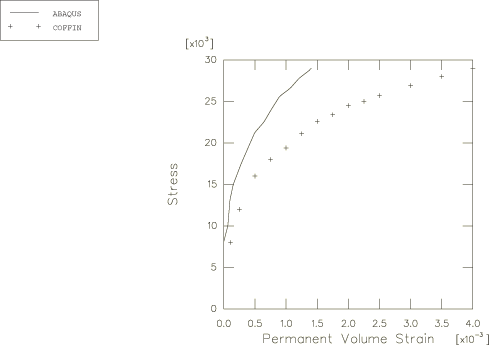
The results for equibiaxial tension are presented in
Figure 6
and
Figure 7.
At high stress values
Abaqus
predicts a stiffer response. The error in the stress/strain response is about
20% at 70% of the fracture stress and higher for higher stress values. The
error in the stress/strain response at high stresses is probably because the
Rankine yield criterion is only an approximation to the real material behavior
under equibiaxial loading conditions.
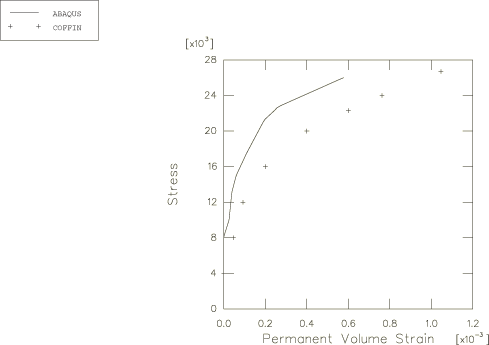
The results for pure shear are shown in
Figure 8
and
Figure 9.
Again,
Abaqus
predicts a stiffer response at high stress values. The error in the
stress/strain response is about 20% at 70% of the fracture stress and higher
for higher stress values. The stress/strain response of the simulation
indicates a change in the rate of hardening at very high stresses. This
behavior is due to a change in the yielding mechanism from Rankine to Mises.
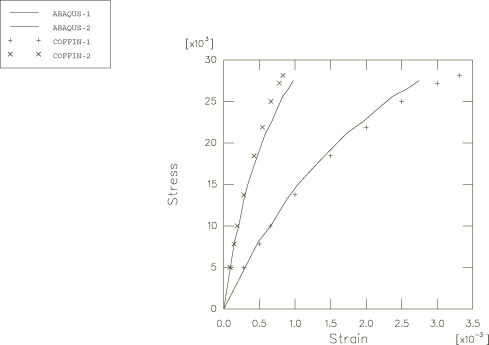
Figure 10
and
Figure 11
show the results for unequal biaxial tension, where the applied loading in one
direction is twice of that in the other. In both the figures the strains are
plotted against the maximum principal stress. In
Figure 10
the curves labeled “Abaqus–1”
and “COFFIN-1” correspond to the maximum
principal stress versus the maximum principal strain, and the curves labeled
“Abaqus–2”
and “COFFIN-2” correspond to the maximum
principal stress versus the intermediate principal strain. The stress/strain
response predicted by
Abaqus
is in good agreement with the experimental results. The difference between the
numerical and experimental results for the permanent volume strain under high
stresses suggests that the minimum principal strain has not been captured as
accurately as the other principal strains in the numerical simulation. The
reason for the better agreement in the stress/strain results for unequal
biaxial tension as compared to those for equibiaxial tension and shear may be
that the loading path is, in relative terms, closer to the uniaxial tension
loading path and that the model is calibrated with uniaxial tension results.
Finally, the case of biaxial tension/compression is shown in
Figure 12
and
Figure 13.
The loading for this test consists of tension in one direction and compression,
with twice the magnitude of the tensile load, in the other direction. The
stress/strain response as predicted by
Abaqus
agrees well with the experimental results. The loading path for this case is
close to the loading path for uniaxial compression, and the model is calibrated
with uniaxial compression results. In
Figure 13
the experimental results indicate a very high value for the maximum permanent
volume change. Given that the loading is predominantly compressive, such a high
value of the permanent volume change is somewhat surprising. It is possible
that such a permanent volume change may be related to effects such as
microbuckling of the graphite flakes; the
Abaqus
model does not capture this behavior.