Air-backed coupled plate response to a planar exponentially decaying wave

This example illustrates the use of Abaqus/Explicit to model the interaction between two fluid-coupled plates and a planar exponentially decaying wave. The results obtained using Abaqus/Explicit are compared with those obtained independently using the Doubly Asymptotic Approximation (Geers (1978), Abaqus/USA 6.1). This problem has been solved analytically by Schechter and Bort (1981).

This page discusses:

ProductsAbaqus/Explicit

Problem description

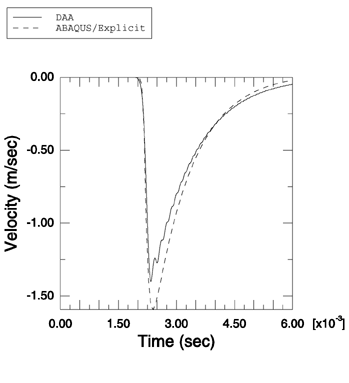
This problem models the interaction between two fluid-coupled elastic plates and a weak planar exponentially decaying shock wave with a maximum pressure of 1.57 MPa and a decay time of 1.0 ms. The second plate (the plate further from the shock source) is air-backed. In contrast to the solution from Schechter and Bort, engineering material parameters for the fluid and solid media are used. Both plates have a square cross-section of side 1 m and a thickness of 0.016 m. The separation between the plates is 3.2 m. The plates are made of steel with a density of 7850 kg/m3, a Young's modulus of 210.0 GPa, and a Poisson's ratio of 0.3. The fluid is water with a density of 1026 kg/m3, in which the speed of sound is 1528 m/s. Each plate is modeled with a single S4R element. A single stack of AC3D8R elements is used to model the fluid in front of the first plate and in between the plates. A planar nonreflective boundary condition is imposed at the end of the outer fluid column using surface impedance. The fluid response is coupled to that of the structure using a tie constraint on the relevant surfaces, with the plate surfaces as main surfaces. The fluid-solid system is excited by a planar exponentially decaying wave applied to the first plate using incident wave loading. A linear bulk viscosity parameter of 0.02 and a quadratic bulk viscosity parameter of 0.5 are used.

Results and discussion

The results from Abaqus/Explicit show good qualitative comparison with those in the referenced literature. We also compare the numerical values for translational velocities of the plates in the direction of the wave obtained using Abaqus/Explicit with those obtained using Abaqus/USA 6.1. As shown in Figure 1 and Figure 2, the results agree closely.

References

  1. Geers,  T., “Doubly Asymptotic Approximations for Transient Motions of Submerged Structures,” Journal of the Acoustical Society of America, vol. 64, pp. 1500–1508, 1978.
  2. Schechter,  R. S.,  and R. L. Bort, “The Response of Two Fluid-Coupled Plates to an Incident Pressure Pulse,” Naval Research Laboratory Memorandum Report, vol. 4647, October 1981.

Figures

Figure 1. Comparison of the translational velocity of the first plate obtained with the Doubly Asymptotic Approximation method and with Abaqus/Explicit.

Figure 2. Comparison of the translational velocity of the second plate obtained with the Doubly Asymptotic Approximation method and with Abaqus/Explicit.