Sensitivity of the stress concentration factor around a circular hole in a plate under uniaxial tension

This example illustrates the design sensitivity analysis capability in Abaqus for a uniaxially loaded plate with a hole. In particular, the sensitivity of the stress concentration to a change in the shape of the hole from circular to elliptical is studied. Since an analytical solution exists, the results are easily verified.

This page discusses:

Problem description
Results and discussion
Input files
Figures

ProductsAbaqus/StandardAbaqus/Design

Problem description

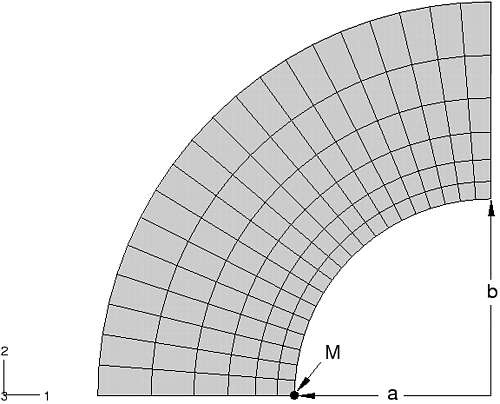
Taking advantage of symmetry, a quarter of a linear elastic square plate with a circular hole is modeled with CPS4 elements. The radius of the hole is 10 units. To simulate an infinite sheet, the plate width is set to 40 times the radius of the hole. A uniaxial tensile pressure P equal to 100 units is applied to the plate in the 2-direction during a linear static step in Abaqus/Standard. The finite element model is shown in Figure 1. The linear static step is followed by a static perturbation step where the load is perturbed by 50 units. Since this problem is linear, the perturbation should produce a sensitivity that is scaled by half.

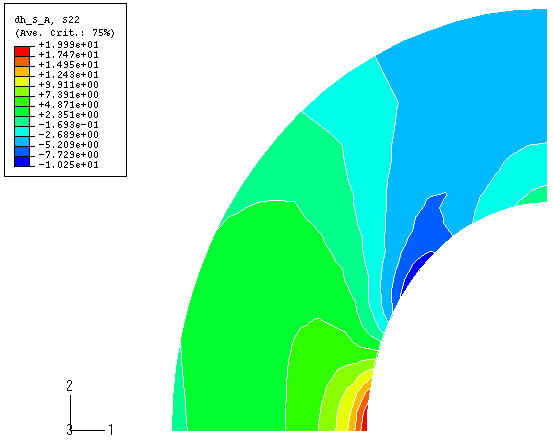
We wish to study the effect of changing the shape of the hole from circular to elliptical on the maximum absolute stress, $σ_{\max}$ ; therefore, the nodal coordinates need to be related to the shape of the hole. Based on experience, the effect of a perturbation in the shape of the hole on the nodal coordinates lying outside the shaded region (shown in Figure 1) can be neglected. The circular hole can be regarded as a special case of an ellipse with its major axis lying along the x-axis. Let a and b represent the semi-major and semi-minor axes, respectively; and consider a point with coordinates $(x, y)$ lying on a circle concentric to the hole. The coordinates of this point can be parameterized as $x = (a + c_{1}) \cos θ$ and $y = (b + c_{2}) \sin θ$ , where $c_{1}$ and $c_{2}$ are constants and $θ$ represents the angle (measured from the positive x-axis) of the position vector to the point from the center of the circle. If the point lies on the boundary of the hole, $c_{1} = c_{2} = 0$ . Positive values of $c_{1}$ and $c_{2}$ move the point into the interior of the plate. The dependence of the nodal coordinates on the parameter a is specified by providing the gradients of x and y with respect to a for the parameter shape variation. The gradients are given as

\frac{d y}{d a} = 0,

and

\frac{d x}{d a} = \cos θ .

Results and discussion

The maximum absolute stress, $σ_{\max}$ , in an infinite plate with an elliptical hole subjected to uniaxial tension $P$ perpendicular to the major axis is given by $σ_{\max} = P (1 + 2 a / b)$ and is the 22-component at the end of the major axis of the ellipse (point M in Figure 2). The contour of $σ_{22}$ in the vicinity of the hole is shown in Figure 3 (shaded elements in Figure 1). The finite element model gives a maximum stress of 299.3 units, which is close to the expected value of 300 units.

The sensitivity of $σ_{22}$ at M with respect to a is given by $d σ_{22}^{M} / d a = 2 P / b$ . The value of $d σ_{22}^{M} / d a$ obtained from Abaqus/Design is 19.99 units and compares well with the analytical result of 20 units. Figure 4 shows the contours of $d σ_{22} / d a$ near the hole. As expected, $σ_{22}$ is most sensitive to the variation in the semi-major axis at points nearest to the region of stress concentration. The value of $d σ_{22}^{M} / d a$ in the perturbation step is 9.995 units, exactly half the value in the linear static step as expected.

Input files

dsastressconcsens.inp: Quarter plate model using CPS4 elements.

Figures