Problem description
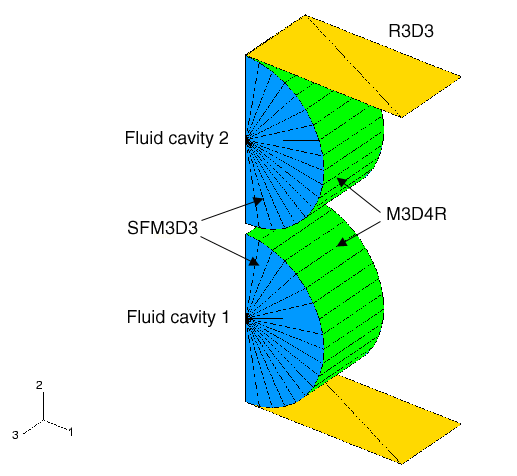
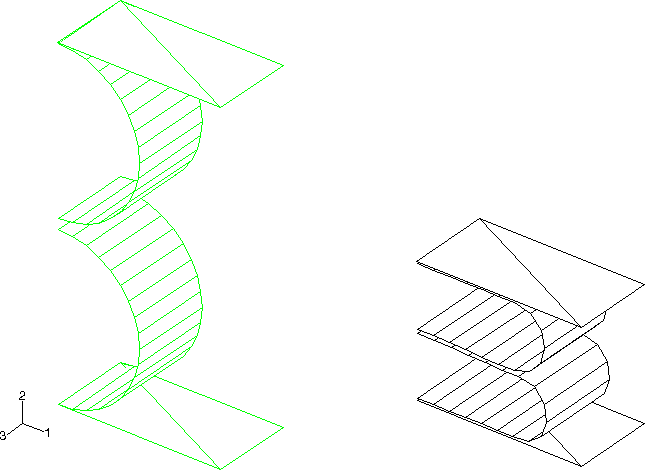
The bladders are modeled as short cylinders (with M3D4R elements) or spheres (with SAX1 elements) with a radius of 1.0 m and a wall thickness of 0.05 m. Ogden hyperelasticity (N=3) with material coefficients calibrated by Abaqus from experimental stress-strain data is used for the rubber constitutive equation. The fluid in the bladders is modeled as fluid cavities. The fluid cavity's reference node must lie on the symmetry plane or the symmetry axis, respectively. The normals to the element-based surface must point into the fluid cavity to obtain the correct cavity volume. The ambient pressure is assumed to be 50.0 kPa, and the fluid is prepressurized to a gauge (additional) pressure of 8.2736 kPa. Static equilibrium requires that the rubber bladders also be subjected to a uniform initial stress of 165.972 kPa along the circumferential direction in the M3D4R elements and a uniform in-plane initial stress of 82.736 kPa in the spheres.
The transfer of fluid is modeled by using a fluid exchange definition and specifying the bulk viscosity for the fluid exchange property. The viscous coefficient, , and the hydrodynamic resistance coefficient, , are chosen to be 10000.0 and 100.0, respectively. These resistance coefficients determine the mass flow rate at any time instant as a function of the pressure differential between the two bladders.