Infinite elements: circular load on half-space

This example of an elastic half-space subjected to a uniform pressure load was suggested by Lynn and Hadid (1981) and examines the performance of different coupled finite/infinite element meshes. The results are compared to the analytical solution given by Timoshenko and Goodier (1970). For comparison purposes a mesh of finite elements only is also used.

This page discusses:

ProductsAbaqus/Standard

Problem description

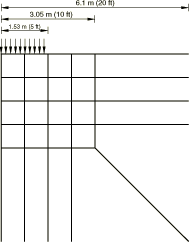
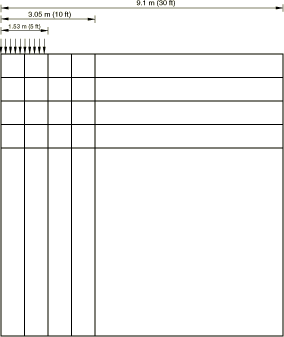
The two finite/infinite element meshes used are shown in Figure 1 and Figure 2. The mesh shown in Figure 1 uses a radial configuration, with the finite elements of the type CAX8R. It extends to a radius of 3 m (10 ft), twice the extent of the load. The far field is modeled with four CINAX5R infinite elements. The second mesh is rectangular, and the finite element part (16 CAX8R elements) also extends to a radius of 3 m (10 ft). Eight CINAX5R elements model the far field. A third mesh of finite elements only is shown in Figure 3: this mesh is identical to the one in Figure 2 with the exception that the outer layer of infinite elements is replaced with a layer of finite elements extending to a distance of 9 m (30 ft), where the normal component of displacement is fixed.

The material is isotropic, linear elastic, with Young's modulus 4.788 MPa (105 lb/ft2) and Poisson's ratio 0.3. The elastic half-space is subjected to uniform pressure load of intensity 4788 Pa (100 lb/ft2) within a radius of 1.5 m (5 ft).

Results and discussion

The analytical solution for this problem is given by Timoshenko and Goodier (1970) and is plotted in Figure 4 and Figure 5. Figure 4 shows the surface deflection as a function of radius, while Figure 5 shows the distribution of vertical stress along a vertical line beneath the center of the load. The displacement results for the meshes with infinite elements show almost exact agreement with the theory, while those obtained with the pure finite elements mesh are correct in form but have an offset from the exact result. The stress results shown in Figure 5 are all in close agreement with the theory.

References

  1. Lynn,  P. P.,  and H. A. Hadid, “Infinite Elements with 1/rn Type Decay,” International Journal of Numerical Methods in Engineering, vol. 17, no. 3, pp. 347–355, 1981.
  2. Timoshenko,  S. P.,  and J. N. Goodier, Theory of Elasticity, McGraw-Hill, New York, 1970.

Figures

Figure 1. Radial finite/infinite element mesh.

Figure 2. Rectangular finite/infinite element mesh.

Figure 3. Mesh of finite elements only.

Figure 4. Surface deflection results.

Figure 5. Vertical stress distribution.