Problem description
The bracket is shown in Figure 1. It is 240 mm long and 30 mm wide, with a thickness of 0.6 mm. The material is linear elastic with Young's modulus E=71240 MPa and Poisson's ratio =0.3. As shown, the bracket is loaded in tension.
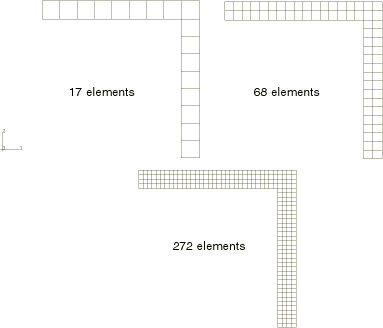
The problem is modeled using fully integrated S4 shell elements with three different meshes: 17, 68, and 272 elements, as shown in Figure 2. For comparison, the finer meshes are also run with reduced-integration S4R shell elements. The reference solution is obtained with a refined mesh of second–order continuum elements. This continuum mesh uses 272 C3D20 elements in-plane and two through the thickness.
To trigger the lateral buckling mode of the bracket, a linear eigenvalue buckling analysis is performed for each model, with the resulting fundamental eigenmode added as an imperfection to the geometry for the nonlinear postbuckling analysis. For this geometry and loading the first eigenmode corresponds to out-of-plane buckling of the bracket when loaded in compression, opposite to the direction shown in Figure 1; the second buckling mode corresponds to tension, the relevant fundamental mode for this analysis. By default, Abaqus calculates both positive and negative eigenvalues, in ascending order of absolute value. To calculate only the positive eigenvalues, use the Lanczos eigensolver and restrict the range of eigenvalues of interest to positive values by setting the minimum eigenvalue of interest equal to zero. This method is particularly useful if the eigenmode is selected as an imperfection for a full geometrically nonlinear analysis; it ensures that the imperfection is appropriate for the direction of loading.