Problem description
The model is the cylinder described in Static analysis for piezoelectric materials. There are nine input files. The input files ppzossd1.inp, ppzossd3.inp, ppzossd4.inp, and ppzossd4a.inp have 16 CAX4E elements. The input file ppzossd2.inp has 4 CAX8E elements. The input files ppzossd7.inp, ppzossd8.inp, and ppzossd9.inp have 32 CAX3E, 8 CAX6E, and 4 CAX8RE elements, respectively.
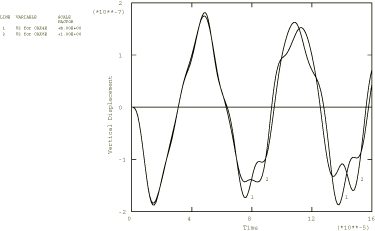
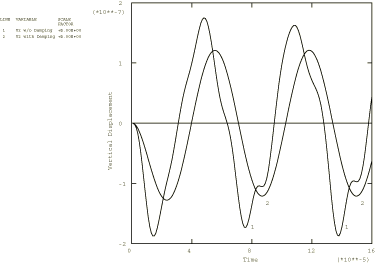
The modal-based steady-state dynamic analyses use the eigendata from the restart files generated in Frequency extraction analysis for piezoelectric materials. The input files ppzossd1.inp and ppzossd2.inp illustrate a steady-state dynamic analysis with no damping and are intended for comparison with the results from Mercer et al. (1987). In this analysis a pressure load is applied on the top surface. In input files ppzossd3.inp, ppzossd7.inp, ppzossd8.inp, and ppzossd9.inp modal damping terms are introduced to the steady-state dynamic analysis mentioned previously to illustrate the effect of damping. Both modal and direct calculation steady-state analyses are performed in input files ppzossd1.inp, ppzossd2.inp, ppzossd3.inp, ppzossd7.inp, ppzossd8.inp, and ppzossd9.inp. The input file ppzossd4.inp illustrates steady-state analysis with a distributed electrical charge, while the input file ppzossd4a.inp performs the steady-state analysis with a concentrated electrical charge instead of the pressure load. Only the direct calculation option is used because the modal-based procedures do not adequately transform the charge loads into modal loads.
In addition to the modal-based and direct-solution analyses, subspace-based steady-state dynamics analyses are performed in the input files ppzossd1.inp, ppzossd3.inp, ppzossd7.inp, ppzossd8.inp, and ppzossd9.inp. An additional frequency step extracts all eigenmodes available, which are then used in the subspace-based steady-state dynamic steps to compute the response. Since all the eigenmodes are used, the results are identical to the ones obtained in the direct-solution analysis.
For all these analyses a single sinusoidal frequency of 100000 rad/sec (15.9 kHz) is chosen to compare to the modal dynamics results from Modal dynamic analysis for piezoelectric materials.