Pressurization of a thick-walled cylinder

This example verifies the use an axisymmetric model, a plane strain model, and a three-dimensional model for a thick-walled cylinder that is loaded with an internal pressure beyond the limit load for the cylinder. The quasi-static solution for this problem is given in Nagtegaal and De Jong (1981).

This page discusses:

ProductsAbaqus/Explicit

Problem description

The cylinder has an inner radius of 1.0 and outer radius of 2.0. The material characterization for the cylinder is assumed to be elastic-plastic with constant isotropic hardening. The material properties are Young's modulus = 1000., Poisson's ratio = 0.3, yield stress = 1., hardening slope = 3., and density = .001.

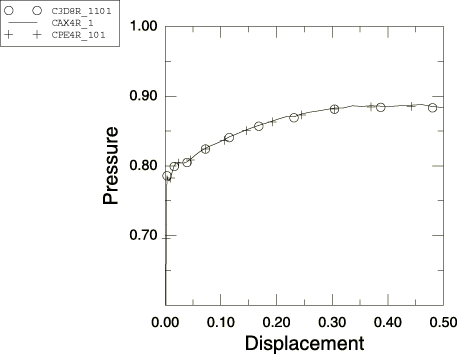
The meshes used in the analysis are shown in Figure 1. In each case there are 20 elements through the thickness of the cylinder.

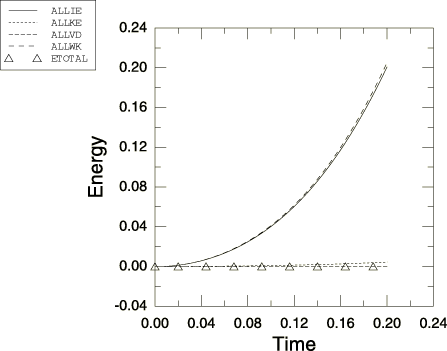
The loading is in the form of displacement control of the nodes on the inner radius of the cylinder. The displacements are of sufficient magnitude that the cylinder becomes fully plastic and exceeds the limit load for the structure. It is not possible to capture the pressure versus displacement curve using pressure loading because of the instability of the structure under the load. Using displacement control, the pressures can be recovered at each (prescribed) displacement point of the inner radius of the structure. To mitigate the dynamic effects in this problem (they cannot be eliminated entirely) the radial velocity of the inner radius nodes is specified as a linear ramp from a velocity of zero to a velocity of 5 over the 0.2 second duration of the steps. The time period of the loading is much longer than the period of any natural mode of vibration of the structure, and the peak velocity is two orders of magnitude lower than the wave speed of the material.

Results and discussion

Abaqus/Explicit models this problem as a transient dynamic analysis. Figure 2 shows the pressure versus radial displacement curves for the three element types used in the analysis. The pressure is inferred from the σx⁢x-component of stress in the first element in each of the meshes. All three cases show some dynamic effects as the cross-section becomes fully plastic. Figure 3 shows the energy balance for this analysis.

Input files

prcyl.inp

Input data used for this analysis.

References

  1. Nagtegaal,  J. C.,  and J. E. De Jong, “Some Computational Aspects of Elastic-Plastic Large Strain Analysis,” International Journal of Numerical Methods in Engineering, vol. 17, pp. 15–41, 1981.

Figures

Figure 1. Meshes for pressurized cylinder problem.

Figure 2. Displacement of inner radius versus pressure.

Figure 3. Energy balance as a function of time.