Force-free motion of a rigid body
Problem description
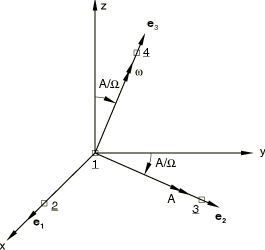
The problem is shown in Figure 1. An arbitrary symmetric body whose rotary inertia about its axis of symmetry is different from its value along the two other principal axes spins around its axis of symmetry with an initial angular velocity The body is modeled with a ROTARYI element whose second moments of inertia along its principal axes, (1, 2, 3), have the values and . The axis of symmetry is . Dummy nodes are attached rigidly to the ROTARYI element along the principal axes by using a BEAMMPC so that their displacements can be tracked. Since ROTARYI elements have only rotational degrees of freedom, a MASS element is needed on top of the ROTARYI element to activate translational degrees of freedom at these dummy nodes. Initial conditions are taken from the analytical solution presented below.
For the force-free symmetric body and ; therefore, the Euler's equations reduce to
The last equation can be integrated to give , where is a constant, defined as an initial condition of the problem.
To determine , we take the time derivative of the first equation:
Using the second equation to solve for gives
Similarly,
These equations describe simple harmonic motion with angular frequency
With appropriate initial conditions the solution is , where A is a constant. The corresponding solution for can be found by substituting this solution for into the first of the Euler equations, giving . The corresponding initial conditions are , , . We also choose , , and . These initial rotation conditions give rise to the local orientation indicated in Figure 1. The directions of the principal axes of inertia of the body are defined. We choose 0.25, 1, 2, so that
Initial angular velocities, , must be applied to node 1, and translational velocities, , must be applied to the dummy nodes lying along the legs of the axes of the body. The translational velocity components are obtained from
where is the vector connecting the center of the body (node 1) to one of the nodes along the principal axes (node 2, 3, or 4). This latter initial velocity calculation is performed internally by Abaqus for each dummy node as a result of applying the BEAMMPCs mentioned previously. The model is shown in rigidbodymotion_free.inp.
The dynamic response of the body subjected to the above initial conditions is tracked for two seconds. Large-rotation theory is used, so the principal axes of inertia rotate with the rotation of the ROTARYI element. Rigid body rotary inertia contributes nonsymmetric terms to the system matrix when the motion is in three dimensions. Therefore, we use the unsymmetric equation solver. Numerical damping is removed from the implicit dynamic operator.
Results and discussion
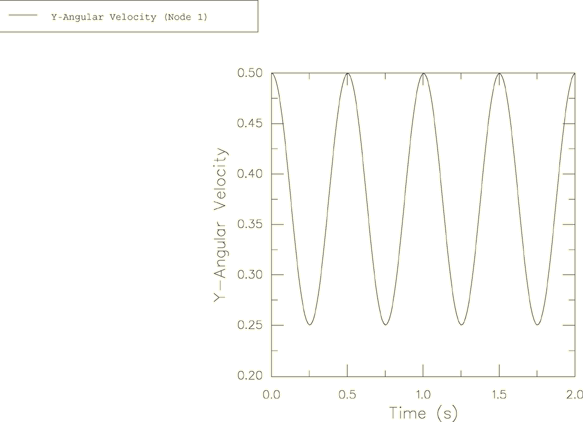
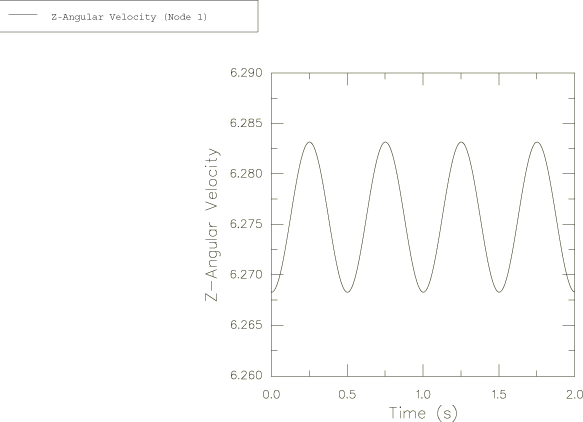
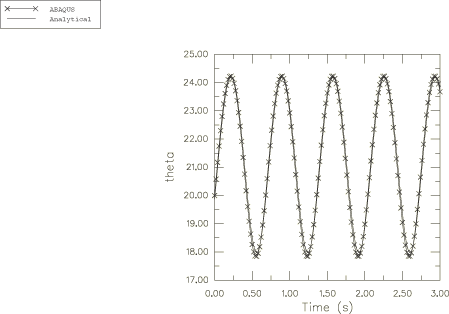
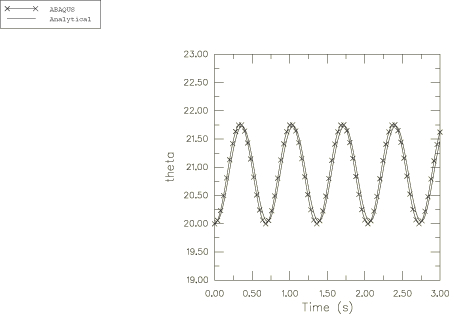
The harmonic response for the angular velocity relative to the global coordinate system is obtained in the Abaqus solution and is plotted in Figure 2, Figure 3, and Figure 4. These angular velocity values are obtained from node 1. Noting that , can be calculated as 6.268. This is shown accurately in Figure 4.
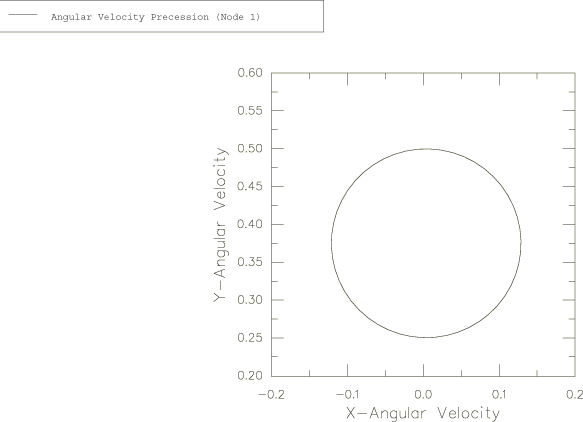
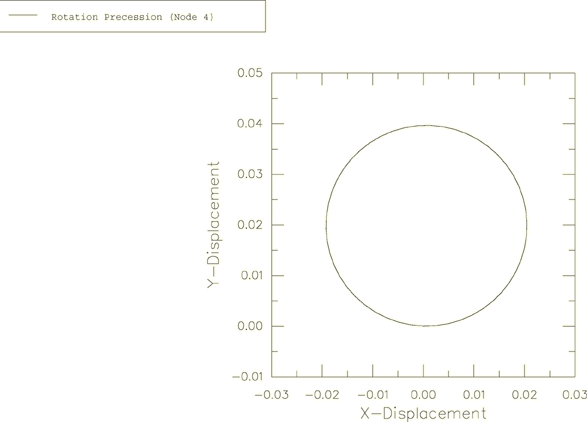
The solutions for and obtained above indicate that the vector + is of constant magnitude and precesses about the body 3-axis with the angular frequency . The evolution of this vector with respect to the global coordinate system is plotted in Figure 5 as an X–Y plot of the history of versus the history of for node 1. As expected, the result traces a circle of diameter A. Figure 6 shows a similar plot of versus for node 4, viewed by looking down the global z-axis.
The precession described by Goldstein is relative to the body axes, which are themselves rotating in space at a frequency of . In large-displacement analysis in Abaqus (geometric nonlinearities considered in the step) the principal axes of inertia rotate with the rotation of the node to which the ROTARYI element is attached. This explains why the period of the motion observed in the figures is 0.5 and not 1.0.
The analysis is completed in 200 increments, with each increment requiring only 1 iteration to satisfy the moment equilibrium criterion.
Input files
- rigidbodymotion_free.inp
-
Implicit force-free motion analysis.
Figures