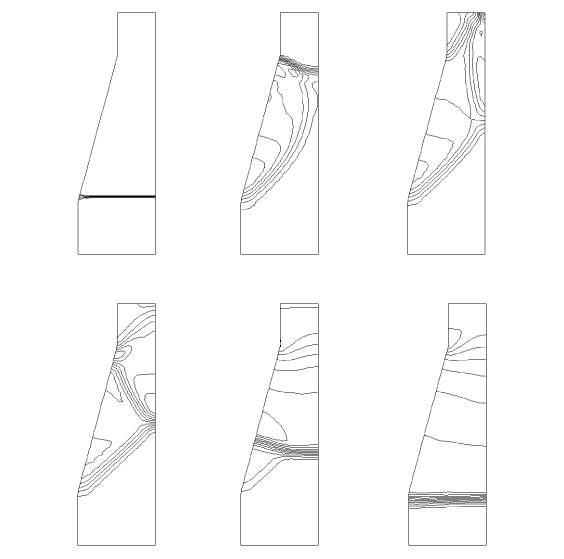
Problem description
A plane shock wave in a gas with negligible viscosity and heat conductivity travels with constant velocity through a two-dimensional channel and encounters a wedge-shaped obstruction on the left wall (Amsden and Ruppel, 1981). A sequence of reflections occurs, depicted qualitatively in Figure 1(a) through Figure 1(e). The event is governed by the theory of regular shock reflection (Harlow and Amdsen, 1971). Figure 1(a) shows the incident shock wave (IS) moving through the channel toward the wedge. A shock wave (WS) is reflected from the wedge as shown in Figure 1(b). The flow Mach number and wedge angle are such that the shock remains attached at the wedge vertex. The wave configuration grows until the reflected shock strikes the right wall of the channel and is reflected back into the channel, as shown in Figure 1(c) (RS). Since the strength and angle of the incident shock wave (IS) are in the Mach reflection regime, a third shock called the Mach stem is formed (MS in Figure 1(d)). The intersection of the three shocks is called the triple point (T). This configuration cannot remain steady, and the Mach stem moves upstream against the incoming flow (Figure 1(e)) and eventually engulfs it, as shown in Figure 1(f).
The wedge half-angle is taken to be 15.13° in this example. A schematic of the model is shown in Figure 2; the model consists of two compartments separated by a diaphragm. Both compartments are filled with the same gas, at different initial states and velocities. The compartments are meshed with CPE4R elements. The left wall of the channel is modeled by a fixed analytical rigid surface, while the right wall is simulated by prescribing a symmetry boundary condition. The Abaqus/Explicit ideal gas equation of state model is used with a gas constant of 0.2 and a constant specific heat at constant volume of 0.5. These constants are not intended to represent any real gases. The gas in compartment A is initially at a unit density, a very small pressure, and zero velocity. Behind the incident shock in compartment B, a high energy gas with an initial density of 6 and an initial pressure stress of 1.2 flows toward compartment A at an initial velocity of 1.0. The diaphragm separating the compartments is removed instantaneously, causing a shock wave to propagate into compartment B.