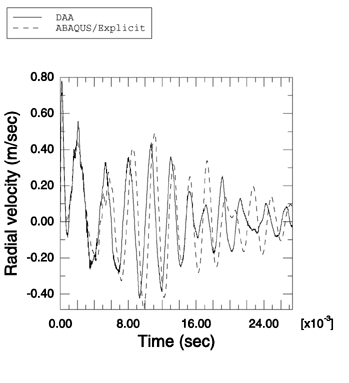
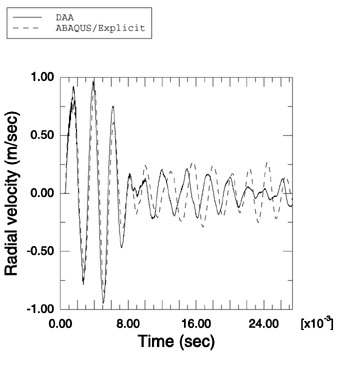
Problem description
This problem models the interaction between an air-backed spherical elastic shell and a weak planar exponentially decaying shock wave with a maximum pressure of 1 MPa and a decay time of 0.685 ms. In contrast to Huang's solution, engineering material parameters for the fluid and solid media are used. The sphere has a radius of 1 m and a thickness of 0.02 m. The sphere is made of steel with a density of 7766 kg/m3, a Young's modulus of 210.0 GPa, and a Poisson's ratio of 0.3. The fluid is water with a density of 997 kg/m3, in which the speed of sound is 1461 m/s. An axisymmetric model is used for this analysis. The spherical shell is represented by a semicircular shell, and the surrounding fluid is represented by an acoustic region bounded by two concentric semicircles and the axis of symmetry. The spherical shell is modeled with SAX1 elements, while the surrounding fluid is modeled with ACAX4R elements. The inner semicircle that bounds the fluid region is coincident with the shell, and the outer semicircle has a radius of 3 m. A spherical nonreflective boundary condition is imposed on the outer semicircle using surface impedance. The fluid response is coupled to that of the structure using a tie constraint. The fluid-solid system is excited by a planar exponentially decaying wave applied at the point where the semicircular shell intersects the axis of symmetry using incident wave loading. A linear bulk viscosity parameter of 0.2 and a quadratic bulk viscosity parameter of 1.2 are used.