Transient response of a shallow spherical cap

This example illustrates the transient response of a shallow spherical cap subjected to uniform pressure.

This page discusses:

ProductsAbaqus/Explicit

Problem description

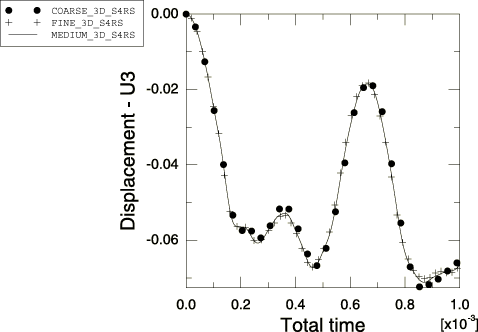
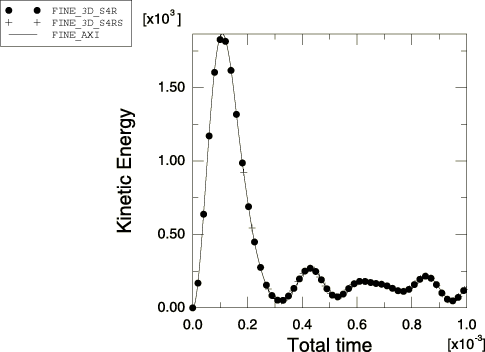
The spherical cap has a radius of 22.27 in. and a thickness of 0.41 in. The response of the spherical cap (shown in Figure 1) is dominated by bending. Both an axisymmetric and a three-dimensional analysis are performed. The three-dimensional model consists of a quadrant modeled with S4R or S4RS elements with appropriate symmetry boundary conditions (see Figure 2).

The material is modeled as an elastic-plastic material with the following properties:

Young's modulus = 10.5 × 106 psi
Poisson's ratio = 0.3
Density = 2.45 × 10−4 lb-sec2/in4
Initial yield stress = 240000 psi
Hardening modulus = 0.21 × 106 psi

A uniform pressure of 600 psi is applied over the shell as a step function in time. Three meshes are used for each geometry. The three-dimensional analysis is performed using 75, 147, and 243 S4R and S4RS elements; and the axisymmetric analysis is performed using 20, 40, and 60 SAX1 elements.

Results and discussion

Figure 3 and Figure 4 show the time histories of the center displacement of the spherical cap predicted by the three-dimensional S4R and S4RS models, respectively. Figure 5 shows some predictions from the axisymmetric models. Figure 6 shows a comparison of the time histories obtained with the finest axisymmetric mesh and the finest three-dimensional mesh. Figure 7 shows a comparison of the time history of the kinetic energy obtained with the finest axisymmetric and three-dimensional meshes.

The results indicate that the SAX1 element, the S4R element, and the S4RS element converge for this problem. They compare well with the existing solutions in the literature (see Bathe et al., 1975, and Belytschko et al., 1984).

Input files

sphr_axa_fine.inp

Axisymmetric analysis with the fine mesh.

sphr_axa_med.inp

Axisymmetric analysis with the medium mesh.

sphr_axa_coarse.inp

Axisymmetric analysis with the coarse mesh.

sphr_coarse.inp

Three-dimensional analysis with the coarse mesh using S4R elements.

sphr_med.inp

Three-dimensional analysis with the medium mesh using S4R elements.

sphr_fine.inp

Three-dimensional analysis with the fine mesh using S4R elements.

sphr_coarse_s4rs.inp

Three-dimensional analysis with the coarse mesh using S4RS elements.

sphr_med_s4rs.inp

Three-dimensional analysis with the medium mesh using S4RS elements.

sphr_fine_s4rs.inp

Three-dimensional analysis with the fine mesh using S4RS elements.

References

  1. Bathe,  K. J., et al.., “Finite Element Formulations for Large Deformation Dynamic Analysis,” International Journal for Numerical Methods in Engineering, vol. 9, pp. 353–386, 1975.
  2. Belytschko,  T. B., et al.., “Explicit Algorithms for the Nonlinear Dynamics of Shells,” Computational Methods in Applied Mechanics and Engineering, vol. 42, pp. 225–251, 1984.

Figures

Figure 1. Geometric characteristics of the spherical cap.

Figure 2. Finest mesh used in the three-dimensional analysis.

Figure 3. Convergence of the center displacement of the spherical cap using S4R elements.

Figure 4. Convergence of the center displacement of the spherical cap using S4RS elements.

Figure 5. Convergence of the center displacement of the spherical cap using SAX1 elements.

Figure 6. Comparison of the time history of the center displacement of the spherical cap for the fine S4R, the fine S4RS, and the fine SAX1 meshes.

Figure 7. Comparison of the time history of the kinetic energy of the spherical cap for the fine S4R, the fine S4RS, and the fine SAX1 meshes.