TEAM 2: Eddy current simulations of long cylindrical conductors in an oscillating magnetic field

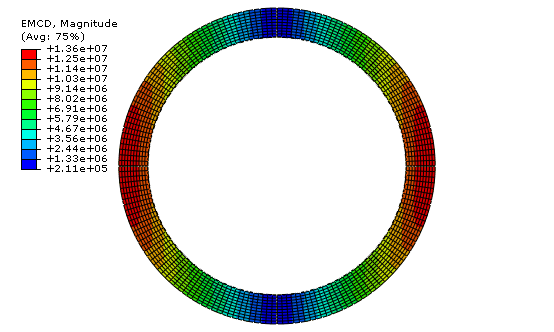
The magnetic vector potential formulation is used to solve this problem. Due to the invariance of the geometry along the $z$-direction and the fact that magnetic flux density lies in the x–y plane, only the $z$-component of magnetic vector potential is nonzero. Although the geometry is two-dimensional in nature, the magnetic vector potential formulation in two dimensions can only represent the $x$- and $y$- components of the magnetic vector potential. Hence, a three-dimensional geometry that contains one element along the $z$-direction is used.

Due to the symmetry of the problem, it is sufficient to model the first quadrant of the problem domain in the x–y plane. Appropriate boundary conditions are imposed on the symmetry planes $x=0$ and $y=0$. Since the magnetic vector potential, $\mathbf{A}$, is oriented along the $z$-direction, symmetry arguments require that it be identically zero on the $x=0$ plane. As a result, a homogeneous Dirichlet boundary condition $\mathbf{A}\times \mathbf{n}=\mathbf{0}$ is applied on the symmetry plane $x=0$. Here $\mathbf{n}$ represents the unit normal perpendicular to the boundary surface. Similarly, on the plane $y=0$, symmetry arguments require that the magnetic field $\mathbf{H}$ be perpendicular to the plane. Hence, a homogeneous Neumann boundary condition $\mathbf{H}\times \mathbf{n}=\mathbf{0}$ is applied on the symmetry plane $y=0$.

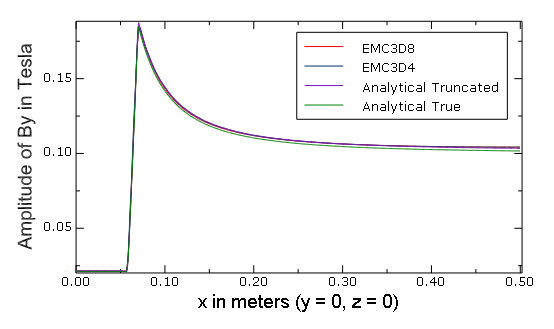
Since the problem domain is unbounded, it must be truncated in some way. Abaqus does not support absorbing boundary conditions; therefore, the truncation boundary should be chosen far away from the conductor. Boundary surfaces far away from the conductor are chosen such that they are parallel to either the $x=0$ or $y=0$ plane. Magnetic vector potential and magnetic flux density far away from the conductor are given by $\mathbf{A}\approx -B_{0}x{\mathbf{e}}_3$ and $\mathbf{B}\approx B_0{\mathbf{e}}_2$, where ${\mathbf{e}}_2$ and ${\mathbf{e}}_3$ are the unit vectors along the $y$- and $z$- coordinate axes. Since the projection of the magnetic vector potential onto the far boundary surface that is parallel to the $x=0$ plane is constant, an inhomogeneous Dirichlet boundary condition $\mathbf{A}\times \mathbf{n}=\mathbf{constant}$ is applied on this boundary surface. Since the magnetic flux density is perpendicular to the far boundary surface that is parallel to the $y=0$ plane, a homogeneous Neumann boundary condition is applied on this boundary surface.

Finally, since the magnetic vector potential is oriented along the $z$-axis, a homogeneous Dirichlet boundary condition is applied on the boundary surfaces that are parallel to the $z=0$ plane.

The magnetic vector potential in various regions of the problem can be expressed as follows:

where $C_i$, $i=1,\mathrm{\cdots },5$ are the constants to be determined; $J_{\nu }\left(x\right)$ and $Y_{\nu }\left(x\right)$ are the cylindrical Bessel functions of the first and second kind, respectively; and $k=\sqrt{-i\omega {\mu }_0{\mu }_r\sigma }$ is the complex wave number of the conductor. Enforcing continuity of the normal component of magnetic flux density and the tangential component of magnetic field intensity on the inner and outer surfaces of the cylindrical shell and applying an inhomogeneous Dirichlet boundary condition on an outer cylindrical surface of radius $c$ leads to the following set of relations between the constants:

where the primed function $Z_{\nu }^{\prime }\left(x\right)$ denotes the first derivative of the function with respect to its argument. In the limit of $c\to \mathrm{\infty }$ we obtain the true solution to the problem. For comparison with the simulation results, truncated analytical results are generated by choosing the value of $c$ to be the distance from the origin to the outer boundary of the problem domain.