Truss impact on a rigid wall

Verification for this problem is provided by comparing the values of significant problem variables with the analytical solution. The numerical solutions are based on the default time incrementation except where noted.

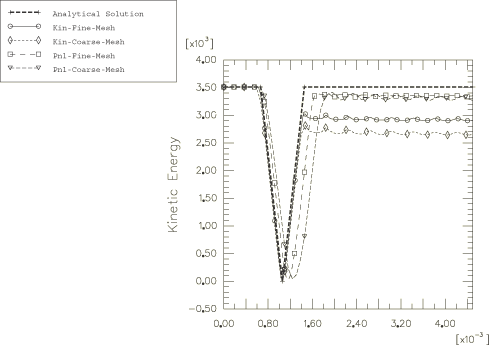
Plots of kinetic energy are shown in Figure 4. Four stages of the solution (pre-impact, truss compression, truss re-expansion, and postimpact) are apparent in this plot. When penalty contact is used, the latter stages are delayed and changes in the slope at the transitions between these stages are smoothed. The onset of truss compression is advanced in time by one increment with kinematic contact. In each of the numerical solutions the kinetic energy is not entirely recovered upon rebound because of the numerical dissipation of energy and finite discretization. For the penalty contact solutions the dissipation of energy is primarily caused by small amounts of bulk viscosity (included by default in the Abaqus/Explicit element formulations) and viscous contact damping (included by default for penalty contact). For the kinematic contact solutions both the bulk viscosity and the contact algorithm itself contribute significantly to the loss of energy. The kinematic contact algorithm dissipates the kinetic energy of the contact node upon impact, whereas the penalty contact algorithm converts the kinetic energy of the contact node into energy stored in the stretched penalty spring. These energy transfer considerations will be discussed further in the following paragraphs.

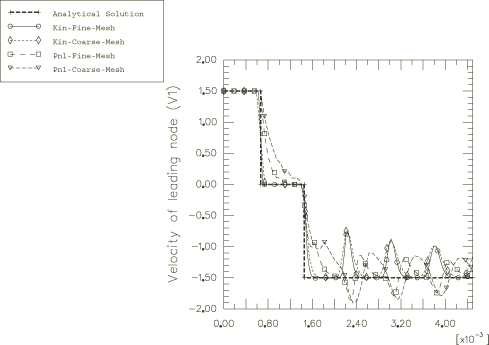
Velocity histories of the leading truss node (contact node) are plotted in Figure 5. The kinematic contact solutions for velocity closely match the analytical solution during pre-impact and during impact. The impact stage is less distinct in the velocity plots for penalty contact because some penetration occurs. All numerical solutions for the postimpact velocity show some oscillations that are not part of the analytical solution. These oscillations are associated with the energy dissipation and finite discretization. In the kinematic contact solutions a stress wave continues to pass through the truss during the postimpact phase, which periodically reduces the magnitude of the nodal velocity. This wave becomes narrower as the mesh is refined. With penalty contact a postimpact stress wave persists, which causes the postimpact nodal velocity to oscillate about approximately −1.5 m/s, where the negative velocity indicates movement in the negative x-direction. In all numerical solutions these velocity oscillations become more diffuse over time as a result of the bulk viscosity damping.

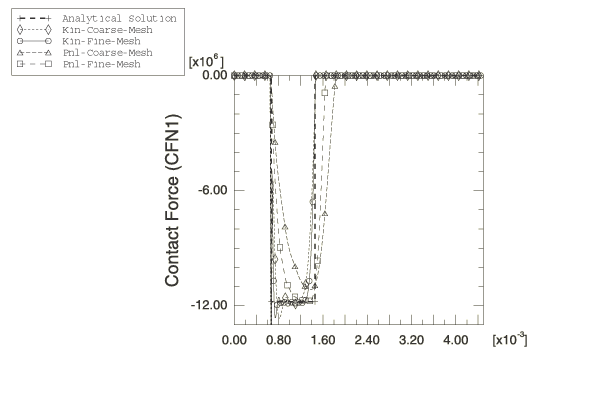
Contact force history solutions are plotted in Figure 6. For the kinematic contact tests Abaqus/Explicit gives very good estimates of the peak contact force and captures the steps in the contact force history quite well. However, it will be shown later that the contact force history with kinematic contact depends on the size of the time increment used in the analysis. The penalty contact force solutions produce reasonable estimates of the peak contact force, but because of the inherent numerical softening of the penalty method, extreme mesh refinement is needed to observe sudden jumps in contact force.

Figure 7 contains plots of external work. The external work remains zero in the analytical solution. Some external work associated with contact forces, which are treated as external forces in Abaqus/Explicit, can be observed in the numerical solutions. With penalty contact the external work accounts for the energy stored in the penalty springs during contact penetration and the energy dissipated by viscous contact damping. After the rebound the external work returns to a constant negative value as the penalty spring energy is recovered; the negative value corresponds to the amount of dissipation due to viscous contact damping. With kinematic contact a contact force first occurs in the increment just prior to the actual impact when a gap is still present; thus, penetration does not occur in the next increment. Therefore, the kinematic contact force does some work when contact is first established. This work corresponds to the kinetic energy of the contact node, and this energy is dissipated by the contact algorithm and is not recovered upon the rebound.

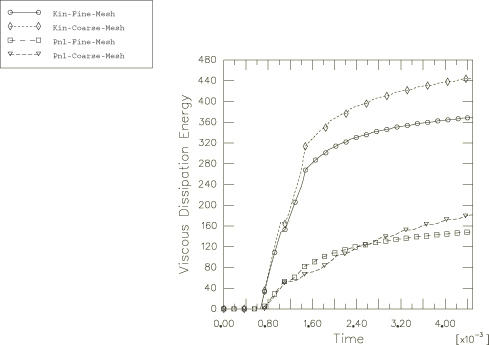
The energy dissipation caused by the bulk viscosity is plotted in Figure 8. This dissipation is greater with kinematic contact than with penalty contact because impacts in the kinematic contact formulation are not softened. Greater shock to the elements and increased element damping occur. Energy continues to dissipate after the rebound as a result of damping of stress waves that persist in the truss after the rebound.

Plots of strain energy are shown in Figure 9. The energy stored in penalty springs is not included in the strain energy reported by Abaqus/Explicit, because the contact forces are treated as external forces. Instead, the energy stored in penalty springs appears as negative external work, as mentioned previously. Some strain energy remains after the rebound in the numerical solutions, which is related to stress waves that remain in the truss.

An undesirable characteristic of the kinematic contact algorithm is that the initial impact force predicted for a given mesh over the contact region depends on the size of the time increment. The contact force results shown in Figure 10 are based on analyses in which the time increment was scaled by 0.25. This scaling simulates the presence of a small element in the model that would control the time increment size. The kinematic contact algorithm will overestimate impact forces if the time increment is significantly lower than the stable time increments of elements near the contact region. Reducing the time increment causes the contact force to increase, because the approach speed of the leading node must be resolved over a shorter time interval to avoid penetration upon impact. Figure 10 also shows that the time increment size has negligible influence on the contact force solution if the penalty contact formulation is used. Other solution variables discussed in this example have minimal dependence on the size of the time increment for both types of contact constraint methods.

To better understand these results, consider a single secondary node impacting a fixed rigid wall. Figure 11 and Figure 12 show such a contact secondary node as a circle in increment $\nu$ . Friction will not be considered.

In the kinematic contact formulation Abaqus/Explicit calculates a predicted penetration $d_{penet}^{pred}$ (see Figure 11). This predicted penetration is equal to the movement of the node if no contact condition is enforced. Abaqus/Explicit then calculates the contact force, $f_{\nu }$, in the normal direction according to

and applies this force in the current increment. The contact force is applied before the contact is actually established. In the next increment, $\nu$+1, the node contacts the surface of the opposing body without penetration (see Figure 11) and the loss of kinetic energy occurs. Although not shown in Figure 11, a contact force will also occur in increment $\nu$+1 in the case of kinematic contact to eliminate the remainder of the velocity component normal to the surface.

Figure 12 shows the schematic for the penalty contact formulation. The contact force is first applied in increment $\nu$+1, and some penetration of the node into the opposing surface occurs. The contact force $f_{\nu +1}$ is calculated according to

where k is the penalty stiffness calculated by Abaqus/Explicit, c is the viscous damping coefficient calculated from the default contact damping setting, and $v_{penet}^{cur}$ is the penetration velocity. The penalty stiffness term can be envisioned physically as a spring attached between the penetrating node and the surface being penetrated. The energy is stored in this spring and is released as the node penetration reverses and decreases to zero (see Figure 7). The small amount of kinetic energy lost (see Figure 4) is the result of viscous effects of the elements, viscous contact damping, and strain energy remaining in the truss after separation (see Figure 9). As the mesh is refined, both formulations tend toward the analytical solution.