One-dimensional underwater shock analysis

The Abaqus model (Figure 1) consists of a single C3D8R continuum element constrained to deform in one dimension. The stiffness and density have been chosen so that the structure alone has a natural frequency of 1 Hz. A single acoustic element is coupled to the structural element. The continuum element has unit cross sectional area and a thickness of 10 units. Two cases are analyzed here. In the first case the acoustic element thickness is set to 0.01 units. In the second case the thickness is increased to 0.1 units. The surface of the acoustic element and the structural element are tied together. The fluid density and speed of sound are both set to 1.0. A plane wave pressure pulse is applied to the front face of the continuum element and the back face of the acoustic element using incident wave loading. The back face of the continuum element is held fixed and a plane wave absorbing boundary condition is specified on the front face of the acoustic element via surface impedance. The pressure pulse travels along the x-axis and is a step function in time. The sound source is located at (100, 0, 0) for the plane waves, and the stand-off point is located at (10, 0, 0). The analysis is run for 10 seconds. The response of the front face of the continuum element is one-dimensional and oscillatory. The analysis is performed in both Abaqus/Standard (u1d_std_c3d8r_ac3d8.inp) and Abaqus/Explicit (u1d_xpl_c3d8r_ac3d8r.inp). There is no damping applied in either the structure or the fluid model except from the radiation boundary condition. However, in Abaqus/Explicit bulk viscosity is used to introduce damping. The value of linear bulk viscosity is chosen as 0.02, and the value of quadratic bulk viscosity is chosen as 0.5.

The model data are kept the same for the restart analysis. In the initial run the loading is applied for 2 seconds. During the restart run, the initial conditions for the new dynamic step are read from the restart files. The loading is applied for 2 seconds. A restart analysis is performed for both Abaqus/Standard and Abaqus/Explicit.

The Abaqus model (Figure 4) consists of a single S4R shell element constrained to translate as a rigid body in one dimension. The planar shell is modeled in the X–Y plane with a length of 1.5 units on all sides. The shell properties are those of steel. A tie constraint is used to couple the structure to the acoustic fluid. The fluid modeled is water. A plane wave underwater pressure pulse is applied to the front face of the structural element and to the back face of the acoustic element. The source is at (0.75, 0.75, 100), and the stand-off point is at (0.75, 0.75, 0). The pulse travels along the z-axis and is a step function in time. The reaction of the plate is rigid body translation in one dimension with constant acceleration. 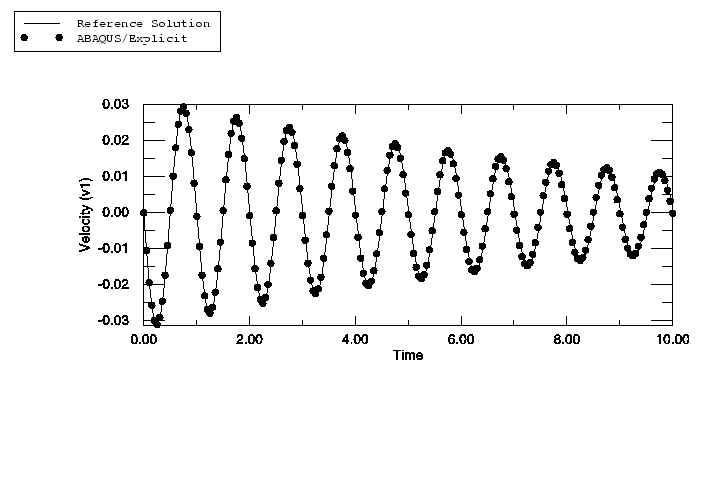The response comparison is based on the velocity time history of the plate. The analysis is performed in both Abaqus/Standard (u1d_std_s4r_ac3d8.inp) and Abaqus/Explicit (u1d_xpl_s4r_ac3d8r.inp).