Infinite cylindrical shell in an infinite fluid
Problem description
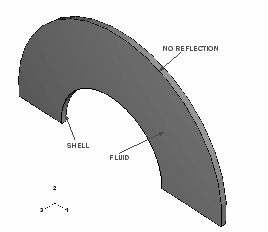
The infinite cylinder excited by a plane wave is a two-dimensional problem with a single plane of symmetry. The half-model for this problem is shown in Figure 1. Plane strain boundary conditions are imposed along the axis of the cylinder, and symmetry boundary conditions are imposed on the x–z plane. Boundary conditions are imposed on the structural model. A consistent set of boundary conditions need not be given for the fluid since they are applied by default. The structure is enclosed in a fluid mesh that models the surrounding fluid. Two different meshes are chosen, and the results are compared. The infinite cylinder is assumed to be fully submerged in the fluid so that free surface effects are negligible. The cylindrical shell is assumed to be made of steel, and the fluid is assumed to be water; however, the material properties have been nondimensionalized. The coupling between the structure and the fluid is enforced using a tie constraint, which does not require compatible meshes. The mesh density for the fluid is chosen such that the shock is captured accurately. The condition for non-reflection is applied on the outer surface of the fluid mesh via the predefined circular radiation boundary condition.
An explosion occurs on the x-axis far from the structure. The incident wave loading is applied at the interface of the structure and the fluid as part of the history data, specifying the location of the charge and the standoff point. Since the front is planar, the charge location is used only to compute the direction of the incoming shock. The standoff point is chosen as the point on the structure closest to the charge, so that the simulation begins when the front is just about to impinge on the structure. The pressure profile of the shock wave measured at the charge standoff point is given by an amplitude curve. For this problem the pressure profile is a step function with a magnitude of 1.0 × 10−4.
The half-cylinder is modeled with 4-node quadrilateral shell elements. In both models the structure is meshed with 36 S4R elements. The fluid meshes are different in the models displaying variations of mesh density. Fluid meshes are modeled with AC3D8R elements. The analyses are run with double precision in Abaqus/Explicit, using direct user control for the time interval. The bulk viscosities and the interval sizes have been specified to optimize the efficiency of the solution, by reducing the run time and capturing the shock accurately.
Results and discussion
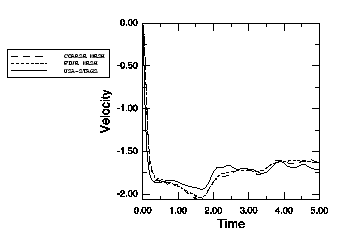
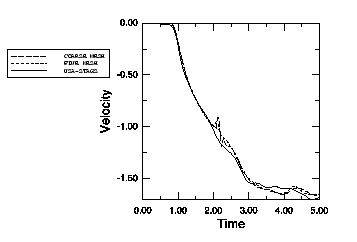
The coarse models use an average mesh size of 0.035 units in the radial direction with each element spanning 10°. In the fine models the average mesh size in the radial direction is 0.02 units, and each element spans 5°. The radiating surface is 2 units away from the center of the shell structure. The results are presented as the value of the radial velocity of the leading node (nearest to the charge, see Figure 2) and the trailing node (farthest from the charge, see Figure 3). The Abaqus results are compared with those obtained using the USA-STAGS program. There is good comparison between the codes.
Input files
- uc_xpl_coarse.inp
-
Coarse mesh model, scattered wave formulation.
- uc_xpl_fine.inp
-
Fine mesh model, scattered wave formulation.
- uc_xpl_tot_coarse.inp
-
Coarse mesh model, total wave formulation.
- uc_xpl_tot_fine.inp
-
Fine mesh model, total wave formulation.
References
- Private Communication, 1990.
- “The Underwater Shock Analysis Code and its Applications,” 60th Shock and Vibration Symposium Proceedings, vol. 1, pp. 89–107, 1989.
- “Underwater Shock Analysis of Nonlinear Structures, A Reference Manual for the USA-STAGS Code (Version 3),” DNA 5545F, Defense Nuclear Agency, Washington D.C., 1980.
- “Scattering of a Transient Acoustic Wave by an Elastic Cylindrical Shell,” Journal of the Acoustical Society of America, vol. 51, no. 5 (part 2), pp. 1640–1651, 1972.
Figures