The submerged sphere problem

This example verifies the use of the underwater shock simulation capabilities of Abaqus to model a submerged spherical shell structure excited by a planar sphere shock wave with a step function profile (plane wave). The response of the submerged spherical shell has been analytically calculated by Huang (Huang and Mair, 1996). In this example the test problems are analyzed using both the total and scattered wave formulations, and the results calculated by Abaqus/Explicit are compared to analytical results.

This page discusses:

ProductsAbaqus/Explicit

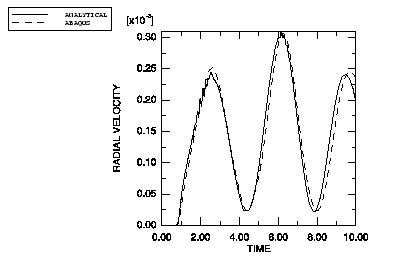
Problem description

The quarter-sphere model is shown in Figure 1. The sphere is entirely submerged in a fluid, deep enough so that free surface effects are unimportant. The figure shows the sphere modeled with 4-node shell elements, enclosed in a fluid mesh modeled with acoustic fluid elements. The material properties used are based on a steel spherical shell and water as the fluid, but the properties have been nondimensionalized. Symmetry boundary conditions are imposed on the structural model. A consistent set of boundary conditions need not be given for the fluid since they are applied by default. The coupling between the structure and the fluid is enforced using a tie constraint, which does not require compatible meshes. The mesh density for the fluid is chosen such that the shock is captured accurately. The condition for non-reflection is applied on the outer surface of the fluid mesh via the predefined spherical radiation boundary condition.

An explosion occurs on the y-axis far from the structure. The incident wave loading is applied to the structure and the fluid at their interface as part of the history data, specifying the location of the charge and the standoff point. Since the front is planar, the charge location is used only to compute the direction of the incoming shock. The standoff point is chosen as the point on the structure closest to the charge, so that the simulation begins when the front is just about to impinge on the structure. The pressure profile of the shock wave measured at the charge standoff point is given by an amplitude curve. For this problem the pressure profile is a step function with a magnitude of 1.0 × 10−4.

The sphere has been modeled with 273 S4R shell elements. The fluid has been meshed with 3250 AC3D8R acoustic fluid elements. To capture the shock front accurately, each fluid element measures 0.03 units radially, while it spans 10° in both the polar and azimuthal directions. The elements must be small enough that significant solution features, such as peaks in POR, span at least several elements. If the computed results show POR (or corresponding structural degrees of freedom) varying greatly over less than several element lengths, mesh refinement is probably required.

Results and discussion

The Abaqus models use time increments of 0.01 units and a total step time of 10 units. The results are presented as the value of the radial velocity of the leading node (nearest to the charge) and the trailing node (farthest from the charge). The Abaqus/Explicit results are shown along with the reference results in Figure 2 and Figure 3. The results compare well in both cases.

Input files

us_xpl.inp

Spherical shell model, scattered wave formulation.

us_tot_xpl.inp

Spherical shell model, total wave formulation.

References

  1. Huang,  H.,  and H. U. Mair, “The ROSEHIPS Program (Response Of a Spherical Elastic Shell to an Incident Plane Step pressure wave) for UNDEX Simulation Validation,” 67th Shock and Vibration Symposium Proceedings, 1996.

Figures

Figure 1. Quarter-sphere shell model.

Figure 2. Leading node velocity time histories.

Figure 3. Trailing node velocity time histories.