Indentation of a thick plate

This example illustrates the use of adaptive meshing and distortion control in deep indentation problems.

This page discusses:

ProductsAbaqus/Explicit

Problem description

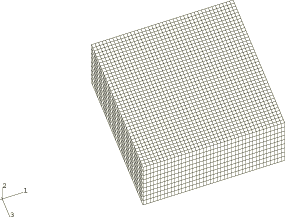
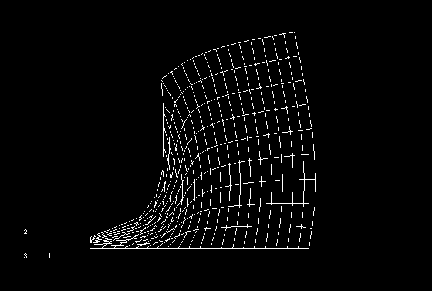
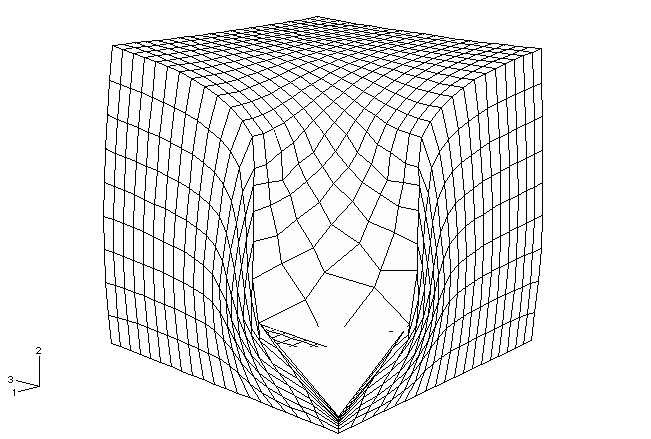
A deep indentation problem is solved for both axisymmetric and three-dimensional geometries, as shown in Figure 1. Each model consists of a rigid punch and a deformable blank. The punch has a semicircular nose section and a radius of 100 mm. The blank is modeled as a crushable foam with the elastic response given as follows (see Schluppkotten, 1999):

E=​ 7.5 MPa (Young's modulus) and
ν=​ 0.0 (elastic Poisson's ratio).

The material parameters for the isotropic hardening are given as

k=σc0/pc0=​ 1.0 (yield strength ratio) and
νp=​ 0.0 (plastic Poisson's ratio),

and the density is

ρ=​ 60 kg/m3.

In both cases the punch is fully constrained except in the vertical direction. A deep indentation is made by moving the punch into the blank to a depth of 250 mm when adaptive meshing is used and to a depth of 285 mm when distortion control is used. The displacement of the punch is prescribed using a smooth-step amplitude so that a quasi-static response is generated.

Case 1: Axisymmetric model

The blank is meshed with CAX4R elements and measures 300 × 300 mm. The punch is modeled as an analytical rigid surface using a planar analytical surface in conjunction with a rigid body constraint. The bottom of the blank is constrained in the x- and z-directions, and symmetry boundary conditions are prescribed at r=0.

Case 2: Three-dimensional models

Two models are analyzed. For one model the blank is meshed uniformly, while for the other a graded mesh is used. For both models the blank is meshed with C3D8R elements and measures 600 × 300 × 600 mm. The punch is modeled as an analytical rigid surface using a three-dimensional surface of revolution in conjunction with a rigid body constraint. The bottom of the blank is fully constrained.

Adaptive meshing

A single adaptive mesh domain that incorporates the entire blank is used for each model. A Lagrangian boundary region type (the default) is used to define the constraints along the bottom of the plate for both models and along the axis of symmetry in two dimensions. A sliding boundary region (the default) is used to define the contact surface on the plate. To obtain a good mesh throughout the simulation, the number of mesh sweeps is increased to 3 as part of the specification of the adaptive mesh domain. For the graded three-dimensional model a graded smoothing objective is specified to preserve the gradation of the mesh while adaptive meshing is performed.

Distortion control

In contrast to the adaptive meshing technique, distortion control does not attempt to maintain a high-quality mesh throughout an analysis but instead tries to prevent negative element volumes or other excessive distortion from occurring during an analysis. By using distortion control, it is possible to prevent an analysis from failing prematurely when the mesh is coarse relative to the strain gradients and the amount of compression. The distortion control capability is tested for axisymmetric and three-dimensional models with a uniformly meshed blank.

Results and discussion

Figure 2 to Figure 4 show the initial configurations for the axisymmetric model, the three-dimensional uniform mesh model, and the three-dimensional graded mesh model. Although the punch is not shown in these figures, it is initially in contact with the plate. Figure 5 shows the final deformed mesh for the axisymmetric indentation. The meshing algorithm attempts to minimize element distortion both near and away from the contact surface with the punch. Figure 6 and Figure 7 show the deformed mesh of the entire blank and a quarter-symmetry, cutaway view, respectively, for the three-dimensional model with an initially uniform mesh. Even under this depth of indentation, elements appear to be nicely shaped both on the surface and throughout the cross-section of the plate.

Figure 8 and Figure 9 show the deformed mesh of the entire plate and a quarter-symmetry, cutaway view, respectively, for the three-dimensional case with an initially graded mesh. Adaptive meshing with the graded smoothing objective preserves the mesh gradation throughout the indentation process while simultaneously minimizing element distortion. Preserving mesh gradation in adaptivity problems is a powerful capability that allows mesh refinement to be concentrated in the areas of highest strain gradients. A contour plot of equivalent plastic strain for the graded mesh case is shown in Figure 10.

Figure 11 shows the final deformed mesh for the axisymmetric indentation using distortion control without adaptive meshing. Figure 12 and Figure 13 show the deformed mesh of the entire blank and a quarter-symmetry, cutaway view, respectively, for the three-dimensional model with an initially uniform mesh using distortion control without adaptive meshing. The distortion control simply prevents element distortion near the contact surface with the punch. Without distortion control both of the analyses fail prematurely under this depth of indentation.

References

  1. Schluppkotten,  J., Investigation of the Abaqus Crushable Foam Plasticity Model, Internal report of BMW AG, 1999.

Figures

Figure 1. Axisymmetric and three-dimensional model geometries.

Figure 2. Initial configuration for the axisymmetric model.

Figure 3. Initial configuration for the three-dimensional model with a uniform mesh.

Figure 4. Initial configuration for the three-dimensional model with a graded mesh.

Figure 5. Deformed configuration for the axisymmetric model.

Figure 6. Deformed configuration for the three-dimensional model with an initially uniform mesh.

Figure 7. Quarter-symmetry, cutaway view of the deformed configuration for the three-dimensional model with an initially uniform mesh.

Figure 8. Deformed configuration for the three-dimensional model with an initially graded mesh.

Figure 9. Quarter-symmetry, cutaway view of the deformed configuration for the three-dimensional model with an initially graded mesh.

Figure 10. Contours of equivalent plastic strain for the three-dimensional model with an initially graded mesh.

Figure 11. Deformed configuration for the axisymmetric model using distortion control.

Figure 12. Deformed configuration for the three-dimensional model with an initially uniform mesh using distortion control.

Figure 13. Quarter-symmetry, cutaway view of the deformed configuration for the three-dimensional model with an initially uniform mesh using distortion control.