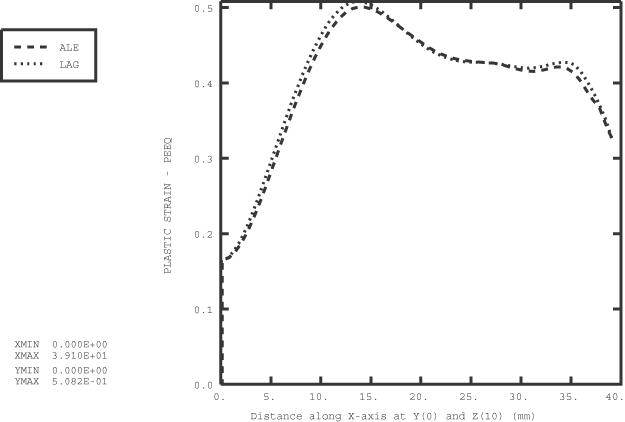
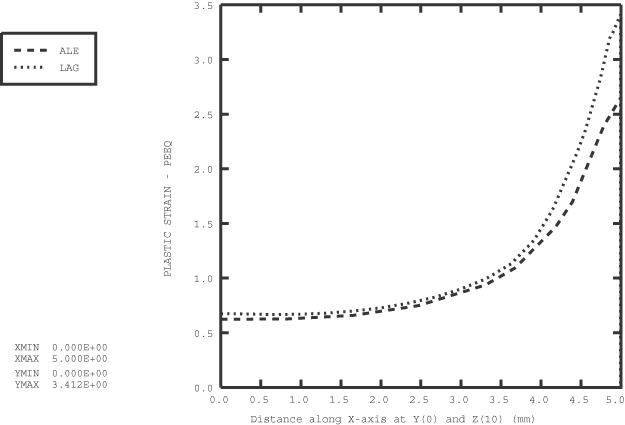
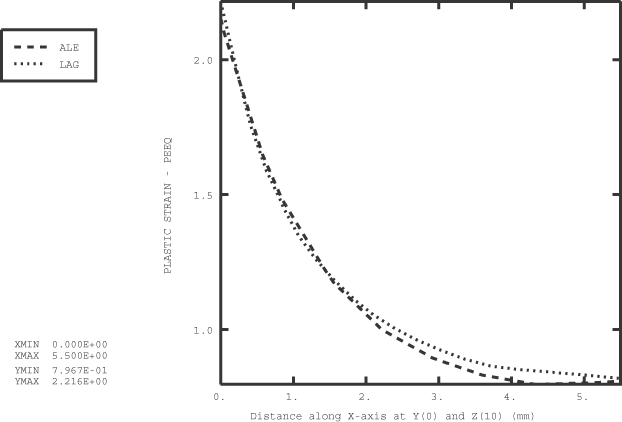
Problem description
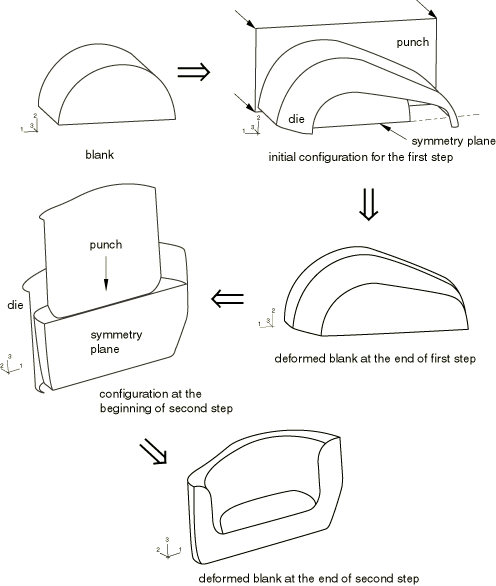
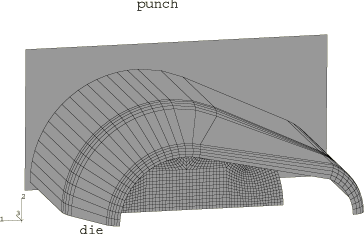
The model consists of two sets of rigid forming tools (one set for each forming step) and a deformable blank. The blank and forming die geometries used in the simulation are shown in Figure 1. The initial configurations of the blank and the tools for each step are shown in Figure 2 and Figure 4. All forming tools are modeled as discrete rigid bodies and meshed with R3D4 and R3D3 elements. The blank, which is meshed with C3D8R elements, is cylindrical and measures 14.5 × 21 mm. A half model is constructed, so symmetry boundary conditions are prescribed at the y=0 plane.
The blank is made of a steel alloy that is assumed to satisfy the Ramberg-Osgood relation for true stress and logarithmic strain,
with a reference stress value (K) of 763 MPa and a work-hardening exponent (n) of 0.245. Isotropic elasticity is assumed, with a Young's modulus of 211 GPa and a Poisson's ratio of 0.3. An initial yield stress of 200 MPa is obtained with these data. The stress-strain behavior is defined by piecewise linear segments matching the Ramberg-Osgood curve up to a total (logarithmic) strain level of 140%, with von Mises yield and isotropic hardening.
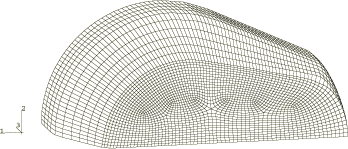
The analysis is conducted in two steps. For the first step the rigid tools consist of a planar punch, a planar base, and a forming die. The initial configuration for this step is shown in Figure 2. The base, which is not shown, is placed at the opening of the forming die to prevent material from passing through the die. The motion of the tools is fully constrained, with the exception of the prescribed displacement in the z-direction for the punch, which is moved 12.69 mm toward the blank at a constant velocity of 30 m/sec consistent with a quasi-static response. The deformed configuration of the blank at the completion of the first step is shown in Figure 3.
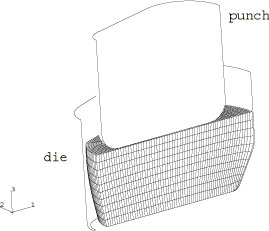
In the second step the original punch and die are removed from the model and replaced with a new punch and die, as shown in Figure 4. The removal of the tools is accomplished by deleting the contact pairs between them and the blank. Although not shown in the figure, the base is retained; both it and the new die are fully constrained. The punch is moved 10.5 mm toward the blank at a constant velocity of 30 m/sec consistent with a quasi-static response. The deformed configuration of the blank at the completion of the second step is shown in Figure 5.