Cask drop with foam impact limiter

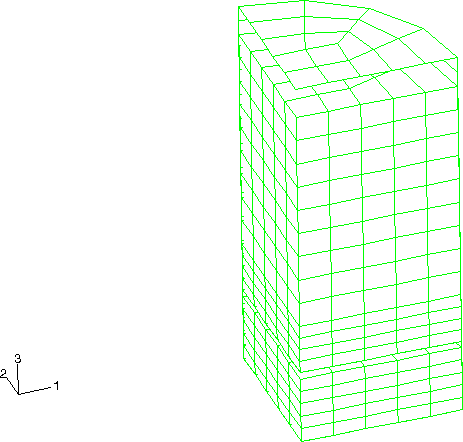
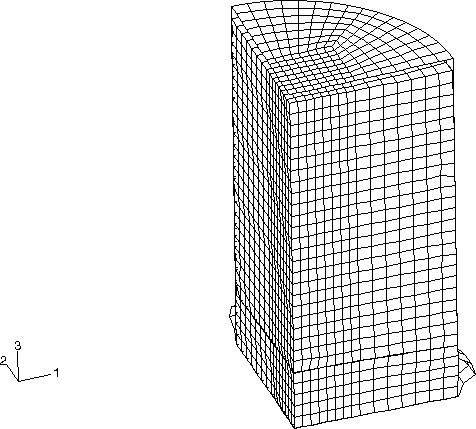
The containment cask shown in Figure 2 consists of two compartments. The upper compartment surrounds the fluid and is made of stainless steel (304L). It has a height of 580 mm (22.8 in), a diameter of 300 mm (11.8 in), and a wall thickness of 4.76 mm (0.187 in). The top mild steel cover has a thickness of 9.52 mm (0.375 in). The water is filled to a depth of 522 mm (20.55 in), which is 90% of the container's capacity. Figure 3 shows the original, coarse mesh of C3D8R elements used to model the fluid. Contact conditions are defined between the fluid and the inside of the upper compartment.

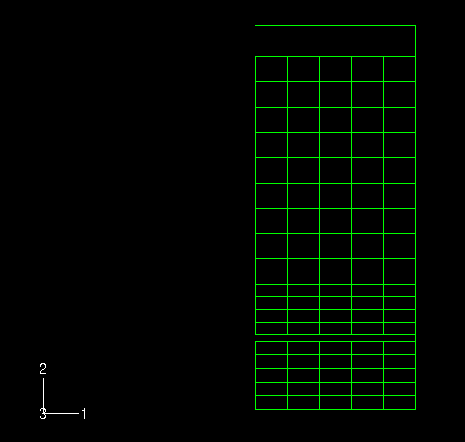
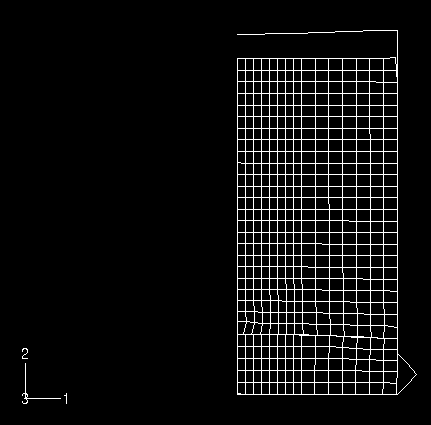
An impact limiter made of polyurethane foam is contained within the bottom mild steel compartment of the cask. The height of the foam impact limiter is 127.3 mm (5.01 in). Figure 4 shows the coarse mesh used to model the foam. Contact conditions are defined between the foam and the inside of the bottom compartment of the cask. The foam impact limiter and the fluid/stainless steel liner are separated by a mild steel bulkhead with a thickness of 12.7 mm (0.5 in). A 12.7 mm (0.5 in) air gap exists between the top of the foam surface and this bulkhead.

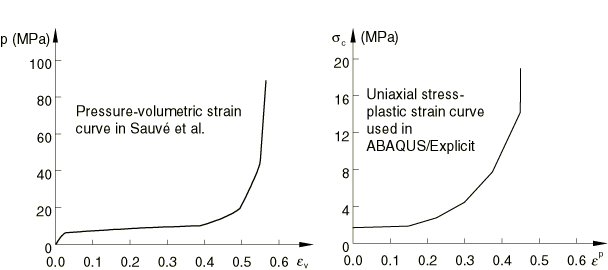
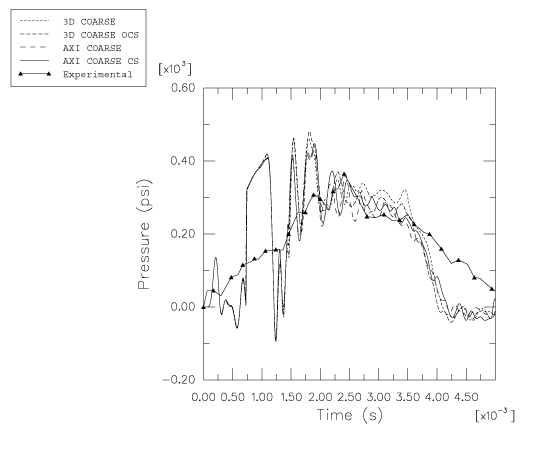
In the experiment a pressure transducer is located in the polyurethane foam on the centerline of the cask at the top of the impact limiter. This result is compared with vertical stress-time histories taken from the element at the top of the foam model on the centerline.

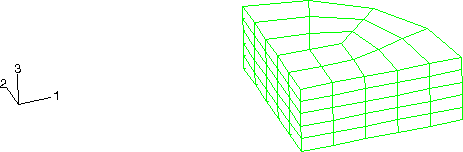
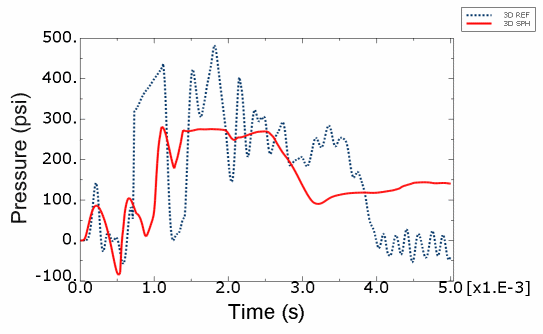
Both axisymmetric and three-dimensional models are analyzed. Figure 5 shows the three-dimensional model formed by assembling the parts shown in Figure 2 through Figure 4. The equivalent axisymmetric model is shown in Figure 6. The corresponding smoothed particle hydrodynamic model incorporates PC3D elements for both the water and the foam parts of the model.

Contact pairs are defined between the solids and the shells. Element-based surfaces are defined on the shells, and node-based surfaces are defined containing the nodes on the outer surfaces of the solid or particle elements. Input files that use the alternative general contact algorithm are also provided. The shell thickness was not taken into account when the original meshes were designed, and the outer surface of the solids usually coincides with the midsurface of the enclosing shell. This would lead to an initial overclosure of one-half the shell thickness, but contact at the midsurface of the shell is enforced, as if the shell had zero thickness. The use of a node-based surface implies a pure main-secondary relationship for the contact pair. This is important in this problem because the default in Abaqus/Explicit when contact is defined between shells and solids is to define a pure main-secondary relationship with the solids as the main and the shells as the secondary. In this case the shell structures are much stiffer than the fluid and foam structures, so the main-secondary roles must be reversed.

For the axisymmetric model two cases using different section controls for the foam and fluid elements are analyzed. The first case uses a linear combination of stiffness and viscous hourglass control; the second case uses the default section controls (the integral viscoelastic form for hourglass control). The three-dimensional model also has two cases with different section controls for the foam and fluid elements. The first case uses the orthogonal kinematic formulation and combined (viscous-stiffness form) hourglass control; the second three-dimensional case uses the default section controls (the average strain kinematic formulation and the integral viscoelastic form for hourglass control). The section controls used are summarized in Table 1. Coarse and refined meshes are used for all analysis cases.

The general material properties are listed in Table 2. The material models for the water and foam are further described below.

Water:

The water is treated as a simple hydrodynamic material model. This provides zero shear strength and a bulk response given by

$$p=K{\epsilon }_{vol},$$

where K is the bulk modulus with a value of 2068 MPa (300000 psi). This model is defined using the linear $U_s-U_p$ equation of state model provided in Abaqus/Explicit. The linear $U_s-U_p$ Hugoniot form, $p=f\left(\rho \right)+g\left(\rho \right)E_m$, is

$$p=\frac{{\rho }_0{c}_0^2\eta }{{\left(1-s\eta \right)}^2}\left(1-\frac{{\mathrm{\Gamma }}_0\eta }{2}\right)+{\mathrm{\Gamma }}_0{\rho }_0{E}_m,$$

where $\eta =1-{\rho }_0/\rho$ is the same as the nominal volumetric strain measure, ${\epsilon }_{vol}$. Since $K={\rho }_0{c}_0^2$, setting the parameters $s=0.0$ and ${\mathrm{\Gamma }}_0=0.0$ gives the simple hydrostatic bulk response defined earlier. In this analysis $c_0=$ 1450.6 m/sec (57100 in/sec) and ${\rho }_0=$ 983.2 kg/m³ (0.92 × 10⁻⁴ lb sec²in⁻⁴). The tension cutoff pressure is assumed to be zero and is specified using a tensile failure model. Refer to Equation of State for a description of this material model.

Foam:

The crushable foam model is used for the polyurethane foam. In this model the flow potential, h, is chosen as

$$h=\sqrt{\frac{9}{2}{p}^2+q^2},$$

where q is the Mises equivalent stress and p is the hydrostatic pressure. The yield surface is defined as

$${\left[{\left(\frac{p_t-p_c}{2}+p\right)}^2+{\left(\frac{q}{M}\right)}^2\right]}^{\frac{1}{2}}=\frac{p_c+p_t}{2}.$$

Sauvé et al. use the “soils and crushable foams” model, which was originally defined in an unpublished report by Krieg (1978) and is based upon a Mises plasticity model in which the yield stress depends upon the mean volumetric pressure. The volumetric deformation allows for plastic behavior, defined by tabular data defining pressure versus volume strain. This model is easy to implement in an explicit dynamics algorithm and useful because the deviatoric and volumetric terms are only loosely coupled. However, it requires an experienced analyst to ensure that meaningful results are obtained, mainly because the model does not match physical behavior well under deviatoric straining.

To define the initial shape of the yield surface, the Abaqus/Explicit crushable foam model with volumetric hardening requires the initial yield stress in uniaxial compression, ${\sigma }_0$; the magnitude of the strength in hydrostatic tension, $p_t$; and the initial yield stress in hydrostatic compression, $p_{c0}$. Sauvé et al. define the pressure-dependent yield surface for the foam model as

$${\sigma }_y^2=3.18+2.06p,$$

where the units of stress are MPa and pressure is positive in compression. To calibrate the Abaqus/Explicit crushable foam model to this pressure-dependent data, we observe that $p=\frac{1}{3}{\sigma }_y$ for the uniaxial compression case. Substituting this value for p in the above equation and solving for ${\sigma }_y$ gives ${\sigma }_0$ = 2.16 MPa (313.3 psi). The value of $p_t$ is obtained by solving the above equation for ${\sigma }_y=0$, giving $p_t$ = 1.54 MPa (223.8 psi). The value of $p_{c0}$ is given in the reference as $p_{c0}$ = 5.52 MPa (800.0 psi).

The pressure-volumetric strain data in the reference are given in Table 3. Table 4 shows the uniaxial stress-plastic strain data converted to the form required for the Abaqus/Explicit volumetric hardening model. Each form of the data is plotted in Figure 1.