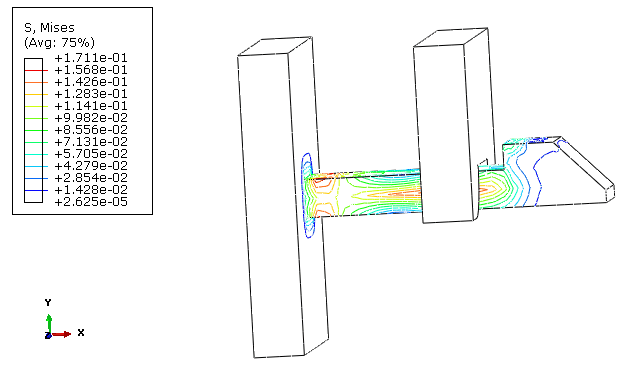
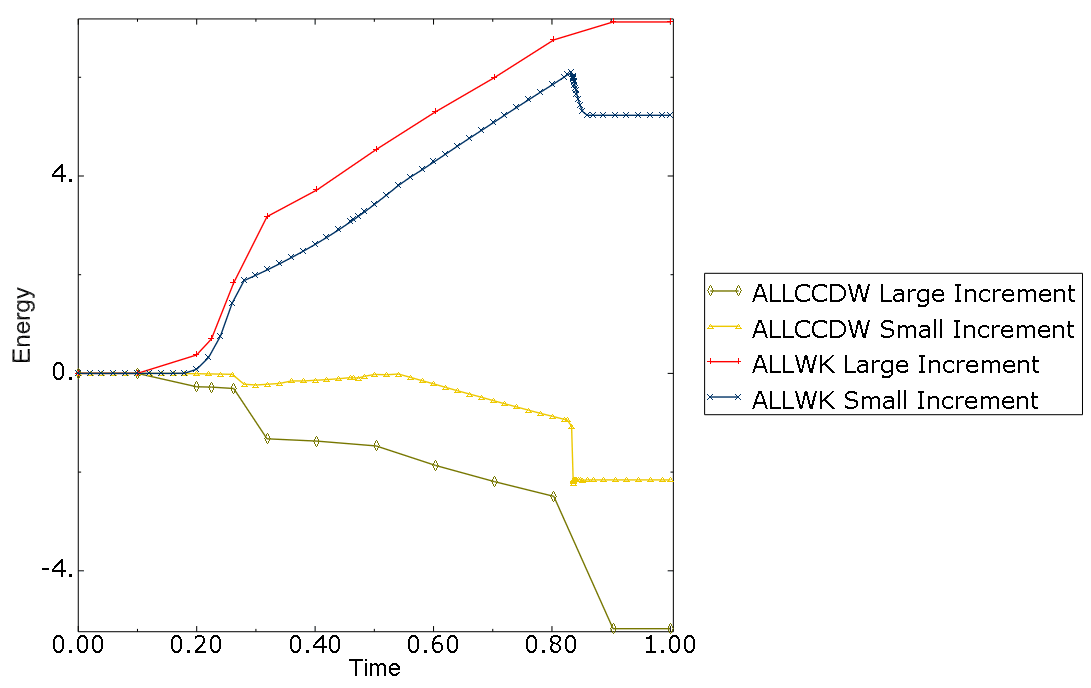
Figure 4
shows a complete set of nonzero energy output variables for this example. The
most significant energies are external work (ALLWK) and contact constraint discontinuity work (ALLCCDW). In this example these output variables have different signs.
If the external work were modified to be ALLWK + ALLCCDW, the major energies would be as shown in
Figure 5.
This combination of ALLWK and ALLCCDW is approximately in balance with the combination of frictional
dissipation and elastic energy throughout the simulation.
The modified external work (ALLWK + ALLCCDW) is often representative of the physical external work in
contact problems in terms of being equal to the sum of the stored and
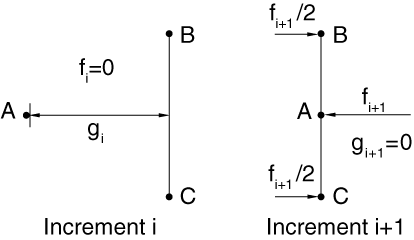
dissipated energies. Consider a particular contact constraint having a gap
distance, ,
in one increment and becoming closed with contact force,
,
in the next increment (see
Figure 6).
A trapezoidal rule for integrating the work done by the contact force
multiplies the average force by the relative incremental motion. In this case
the resulting contribution to ALLCCDW is negative .
This energy contribution is nonphysical and would disappear in the numerics as
the time increment tends to zero. When contact opens up, similar behavior
happens with sign reversals. Numerical integration for ALLWK is also limited with respect to accounting accurately for
sudden changes in external forces. Summing ALLWK and ALLCCDW often cancels the respective nonphysical energy contributions,
and the net effect on the total energy balance (ETOTAL) is zero.
A nonzero incremental ALLCCDW contribution can also occur if the normal direction changes
during a time increment that also has relative motion between contact surfaces.
The first significant drop in ALLCCDW for this example (see
Figure 4)
occurs from increment 4 to increment 5, when the leading wall edge slips from
the inclined arrowhead surface to the top surface, as illustrated in
Figure 7,
causing a significant change in the contact constraint normal direction.
With finer time incrementation, ALLCCDW generally becomes smaller, as demonstrated in
Figure 8.
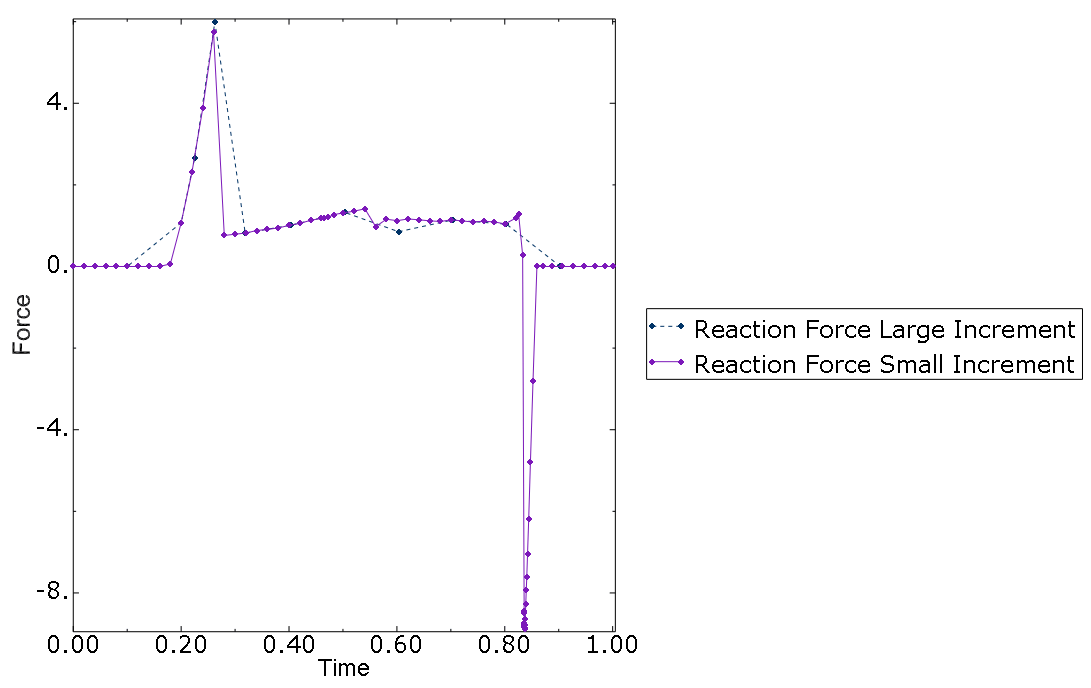
The maximum time increment allowed with so-called large time increments is five
times larger than with small time increments. Convergence of global Newton
iterations is more difficult to reach with small time increments because of the
model behavior near the last stage of the analysis when the arrowhead snaps to
the stress-free state. The “back of the head” touches the rear edge of the wall
along the way, whereas with large time increments, this touching is avoided
completely. The difference is reflected by the reaction force X becoming
negative for small time increments (see
Figure 9).
Elastic contact energies are shown in
Figure 10.
They are small compared to the major energies in the model. If ALLCCEN is not small, contact penalty stiffness may need to be
increased to improve solution accuracy. If ALLCCET is not small, the frictional elastic or slip tolerance may need
to be decreased to increase the frictional penalty stiffness.
Ideally, ETOTAL should be exactly constant (in this example zero), but actually
it is constant only approximately. The approximation is due to the fact that
the recoverable strain energy (ALLIE) is computed by a modified trapezoidal rule, rather than an
exact trapezoidal rule (which is not implemented due to dramatic computational
performance implications). Such behavior is common in geometrically nonlinear
problems, and one can only assess that the variation in ETOTAL is small compared to meaningful energies.
Nonzero initial ETOTAL will (appropriately) occur, for example, when initial stress is
specified, such that the initial value of ALLIE is positive while other energies are initially zero. Nonzero
initial ETOTAL also occurs when initial velocities are defined for a dynamic
analysis; in this case initial kinetic energy is positive.
Convergence tolerances can also influence energy results because the energy
balance depends on the balance of internal and external forces and moments in
the model.