Transient dynamic nonlinear response of a piezoelectric transducer

This example demonstrates the Abaqus capability for predicting the nonlinear transient dynamic behavior of structural systems that incorporate piezoelectric components. The example utilizes a piezoelectric bending-type transducer that is idealized as a simple layered beam structure. The fabrication of the transducer is modeled, and the eigenfrequencies of the preloaded structure are extracted. Finally, the dynamic response due to a transient electrical potential pulse is monitored. Piezoelectric transducers are commonly used in the following application areas:

  • Ultrasonic imaging systems

  • Ultrasonic cleaning systems

  • Ultrasonic welding/bonding systems

  • Audio systems

  • Acoustic transducers

  • Active vibration control systems

This page discusses:

ProductsAbaqus/Standard

Geometry and material

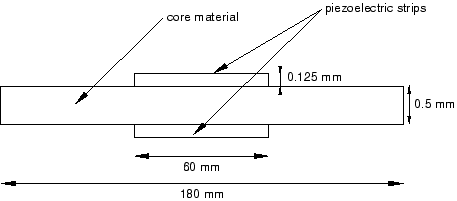
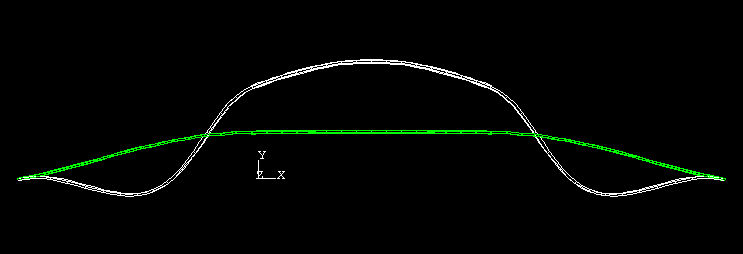
The transducer is shown in Figure 1. It has a composite beam that is 0.0025 m wide and 0.18 m long. The initially straight beam has a 0.0005 m thick insulating core; 0.000125 m thick PZT–5H piezoelectric strips are bonded to the top and the bottom faces of the core material. The piezoelectric strips are only 0.060 m long and are centered at the beam mid-span. The piezoelectric strips are polarized along the beams in the through-thickness direction. The properties for the PZT–5H material are as follows:

Elastic properties:

Engineering constants
E1 60.61 GPa
E2 48.31 GPa
E3 60.61 GPa
ν12 0.512
ν13 0.289
ν23 0.408
G12 23.0 GPa
G13 23.5 GPa
G23 23.0 GPa

Piezoelectric coupling matrix (strain coefficients):

[00074100-274593-27400000000741]⁢10-12    m/volt

Dielectric matrix:

[1.5050001.3010001.505]⁢10-8     farad/meter

The local 1-direction is in the beam longitudinal direction, and the local 2- and 3-directions are in the beam cross-section. From these matrices it can be seen that the poling direction is in the local 2-direction of the piezoelectric strips.

The core material is elastic and isotropic with a Young's modulus of 6 GPa, a density of 1500 kg/m3, and a Poisson's ratio of 0.35.

Model

The beam core material is modeled with 46 C3D20 elements, and the piezoelectric strips are modeled using 16 C3D20E elements each. A perfect bond between the core and the piezoelectric materials is defined with a surface-based tie constraint, for which the piezoelectric surfaces are retained as the main surfaces. The electrical potentials for the top and the bottom surfaces of each piezoelectric strip are coupled to the electrical potentials of the main nodes assigned to each surface using linear constraint equations. The electrical potentials and the reaction charges can be monitored at these main nodes. The piezoelectric surfaces bonded to the core material are assigned a zero electrical potential throughout the analysis.

The first 8 steps are used to represent the fabrication procedure and to investigate the behavior of the fabricated transducer. These include linear perturbation steps to investigate the eigenmodes of the fabricated transducer at various stages during its fabrication. Steps 9 through 11 represent a general nonlinear transient analysis of the transducer. A square wave electrical potential pulse of 200 volts is applied using a boundary condition with a step function amplitude. Immediately after the pulse, a closed circuit condition (potential gradients are prescribed) is maintained and the reaction charges are monitored. Subsequently, the circuit is opened (the potential gradient is not prescribed; the potential is an active degree of freedom that is determined as part of the solution). In the case of an open circuit condition the resulting voltage can be used to measure the transducer's open circuit free vibration. The analysis steps are as follows:

  1. Static shape fabrication: deformation induced via an applied potential of 1000 volts.

  2. Static shape fabrication: fix support ends, and reduce the applied potential to 0 volts.

  3. Closed circuit modal analysis about the base state obtained at the end of Step 2.

  4. Static shape fabrication: apply open circuit conditions.

  5. Open circuit modal analysis about the base state obtained at the end of Step 4.

  6. Static test at an operational load of 200 volts.

  7. Closed circuit modal analysis about the base state obtained at the end of Step 6.

  8. Reset to zero voltage condition.

  9. Transient dynamic response: apply voltage pulse of 200 volts for 0.00265 seconds.

  10. Transient dynamic response: free vibration under closed circuit condition with 0 volts.

  11. Transient dynamic response: free vibration under open circuit condition.

Results and discussion

In Figure 2 the deformed and superimposed undeformed shapes are shown after applying 1000 volts at both piezoelectric strips. In Figure 3 the deformed shape is shown at the end of Step 2, where both ends are fixed and an applied potential of 0 volts is prescribed. Subsequently, the eigenfrequencies are extracted about this preloaded state. In Figure 4 the third eigenmode with a frequency of 150.9 cycles/sec is shown for this closed circuit condition. Figure 5 shows the third mode shape with a frequency of 154.4 cycles/sec under open circuit conditions. The third mode shape for the closed circuit condition with a prescribed voltage of 200 volts is again almost identical to the third mode shape shown in Figure 4. However, the eigenfrequency has changed to 181.7 cycles/sec.

In Steps 9 and 10 a closed circuit condition is prescribed for the piezoelectric strips, and subsequently in Step 11 the voltage boundary conditions are removed resulting in open circuit conditions. Figure 6 shows the time history of the potential under closed and open circuit conditions. Typically, the transducer acts as a “driver” in a closed circuit condition as the potential gradient is prescribed, thereby driving the structure. On the other hand, the transducer acts as a “receiver” in an open circuit condition as the voltage output can be used to measure the mechanical response. In Figure 7 the reaction charge at the top piezoelectric strip is shown under the above conditions. In a closed circuit condition the reaction charge changes in time, while in an open circuit condition the reaction charge is equal to zero. The displacement of the transducer's center is demonstrated in Figure 8.

The results are presented to illustrate the general capabilities in Abaqus for predicting the transient response of piezoelectric structures. If this system represented part of an actual ultrasound system, additional output related to the design/analysis objective would be created and analyzed.

Figures

Figure 1. Geometry of the piezoelectric transducer.

Figure 2. Deformed shape with superimposed undeformed shape at the end of Step 1.

Figure 3. Deformed shape with superimposed undeformed shape at the end of Step 2.

Figure 4. Mode shape 3 with superimposed shape of the base state after Step 2.

Figure 5. Mode shape 3 with superimposed shape of the base state after Step 4.

Figure 6. Transient response of potential at top piezoelectric strip.

Figure 7. Transient dynamic response of the reaction charge at top piezoelectric strip.

Figure 8. Transient response of center displacement.