Geometry and model
The structure consists of 19 members between structural connections. Each finite element models a member of the frame. Hence, 19 frame elements are used: 17 elements with PIPE cross-sections of varying properties and 2 elements (the top platform) with I cross-sections. The plastic response of the elements is calculated from the yield stress of the material, using the plastic default values provided by Abaqus. (The default values for the plastic response are based on experiments with slender steel members. For details on the default values, see Frame Section Behavior.) The default plastic response includes mild hardening for axial forces and strong hardening for bending moments. The default hardening responses for a typical element in the model are shown in Figure 2 and Figure 3.
A dead load of 444.8 kN (100,000 lb) is applied to the top of the K-frame, representing the part of the structure above the K-frame. Subsequently, the top platform is loaded or displaced horizontally. The load level or applied displacement is chosen to be large enough so that the entire structure fails by the formation of plastic hinges and, consequently, loses load-carrying capacity.
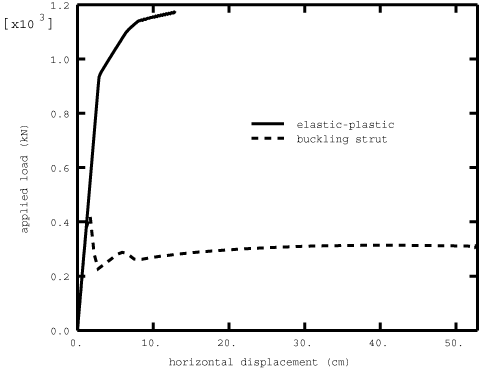
Three different models are investigated. A limit load is expected, since the goal of the analysis is to determine when the structure loses overall stiffness. Large- and small-displacement analyses are performed for all three models for comparison. Large-displacement analyses using frame elements are valid for large overall rotations but small strains, since frame elements assume that the strains are small. In the first model all elements use elastic-plastic material response. In the second model buckling is checked for all elements with PIPE cross-sections. The ISO equation is used as a criteria for buckling, and the default Marshall strut envelope is followed for the postbuckling behavior. The buckling strut envelope is calculated from the yield stress of the material and the default Marshall Strut theory. (For details on the default buckling strut envelope, see Frame Section Behavior.) All frame members that use the buckling strut response check the ISO criteria for the switching-to-strut algorithm. In the third model the member that switches to strut behavior in the second model (element 7) is replaced by a frame element with buckling strut response from the beginning of the analysis. To proceed beyond the unstable phase of the response, the Riks static solution procedure is used in the elastic-plastic problems. To decrease the number of solution iterations, the solution controls are used in the elastic-plastic problem with large displacement, with the value of the ratio of the largest solution correction to the largest incremental solution set to 1.0, since displacement increments are very small after plasticity occurs.