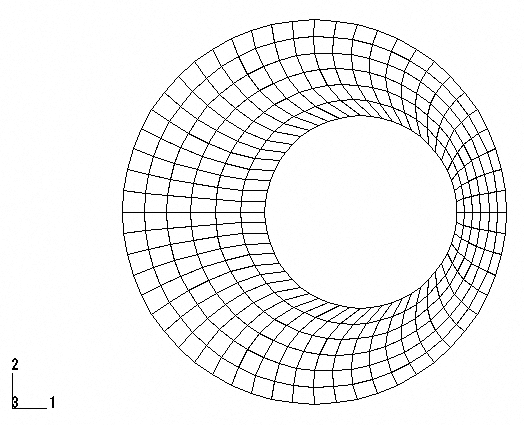
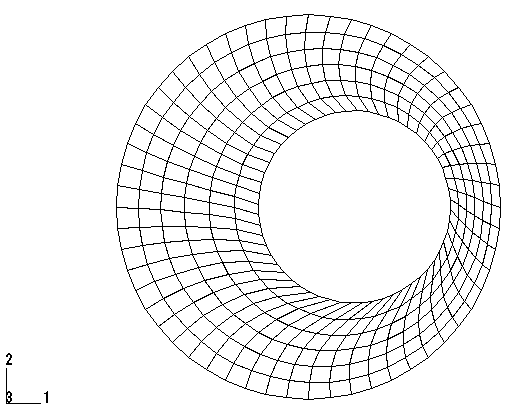
Geometry and model
The viscoelastic bushing has an inner radius of 12.7 mm (0.5 in) and an outer radius of 25.4 mm (1.0 in). We assume that the bushing is long enough for plane strain deformation to occur. The problem is modeled with first-order reduced-integration elements (CPE4R). The mesh is regular, consisting of 6 elements radially, repeated 56 times to cover the 360° span in the hoop direction. The mesh is shown in Figure 1. No mesh convergence studies have been performed.
The fixed outer body is modeled by fixing both displacement components at all the outside nodes. The nodes in the inner boundary of the bushing are connected, using a kinematic coupling constraint, to a node located in the center of the model. This node, thus, defines the inner shaft as a rigid body.