Design sensitivity analysis of a windshield wiper

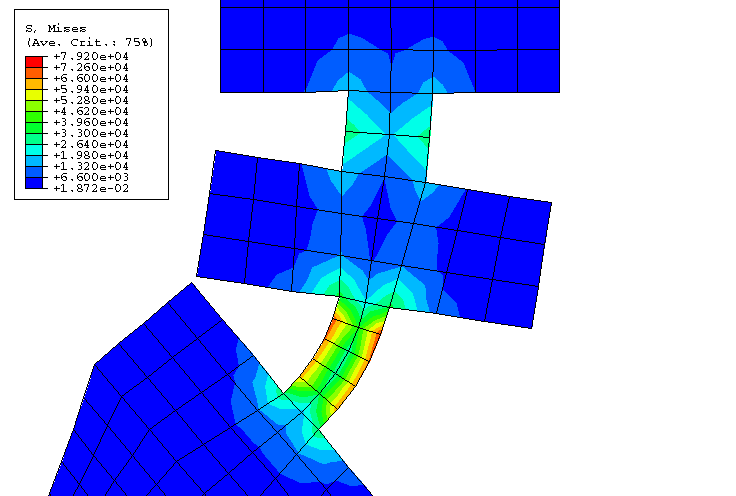
A contour plot of the von Mises stress distribution on the deformed configuration of the rubber blade is shown in Figure 5. It is evident that the two necks between the flanges are the areas of interest. In a magnified contour plot of the von Mises stress distribution in the necks (Figure 6) we can see that the stress concentration in the lower neck is higher than in the upper one. The normalized sensitivities of the maximum von Mises stresses in the lower neck are listed in Table 1. Sensitivities are normalized by dividing them by the maximum Mises value (67857.7 units in element 131 of the wiper blade) and then scaling the result by the initial value of the design parameter. We notice that the shape parameters have a direct effect (increasing the parameter increases stress and vice versa) and the friction coefficient has an inverse effect on the von Mises stress. Reducing the thickness of the neck makes the wiper more flexible and reduces stress concentration. Increasing the friction coefficient increases the shear force at the tip. This increased shear force increases bending of the upper neck and decreases bending in the lower neck, thus reducing the stress concentration in the lower neck. We infer from the table that the von Mises stress is more sensitive to $t2$ and $t3$ than to the flange width and friction coefficient. To reduce stress concentration, a design with changes in $t2$ and $t3$ is considered. A 20% reduction in $t2$ and a 10% reduction in $t3$ is selected. The predicted percentage reduction in the von Mises stress is 6.76 (0.2832 × 0.2 + 0.1094 × 0.1).

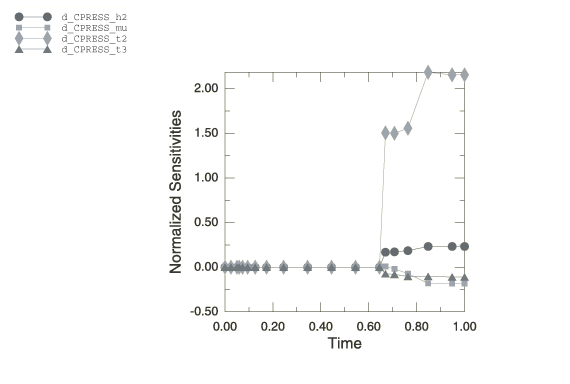
The proposed design changes will affect the contact pressure at the wiper-windshield interface, and the sensitivity results are used to quantify this effect. The time history of the normalized sensitivities of contact pressure at a point at the tip is shown in Figure 7. Contact pressure at this point is most sensitive to $t2$. This result is somewhat unexpected since this design parameter does not affect the interface explicitly. $t2$ has a directly proportional effect, while $t3$ has an inversely proportional effect on the contact pressures. Thus, decreasing $t2$ will decrease the contact pressure while decreasing $t3$ will increase the contact pressure. The contact pressure histories for the proposed design and the current design are shown in Figure 8. The plots indicate that the reduced stress concentration in the proposed design comes at the cost of decreased wiper performance. (The proposed design has a lower contact pressure, which could be suboptimal.) If desired, the contact pressure can be positively influenced by considering a positive change in $t3$.

All results discussed above are obtained in an incremental DSA analysis using the unsymmetric solver. If the user is interested only in the results at particular increments (typically, the last increment), total DSA will be advantageous computationally. Similarly, neglecting the unsymmetric terms will improve computational efficiency. To quantify the error in such approximations, we compare the results for various combinations to the overall finite difference method (OFD). Table 2 lists the relative error in the maximum Mises and contact pressure sensitivities compared to the results obtained using the OFD method. For the dominant shape parameter, $t2$ , the sensitivity results of the maximum von Mises stress are in good agreement with the OFD method for all the combinations. However, neglecting the unsymmetric terms in total DSA gives inaccurate results for the contact pressure sensitivities. The relative error is large for the less dominant shape parameters, with total DSA giving poor results for both the Mises and contact pressure sensitivities. Total DSA gives inaccurate results for sensitivities with respect to the friction coefficient. Although the sensitivity results are problem dependent, we can infer that total DSA may give poor results if we neglect unsymmetric terms. Further sensitivities of interaction pressures are more sensitive to approximations than the sensitivities of maximum stresses in the structures. Less significant sensitivities are affected more by approximations than the dominant sensitivities.

The proposed design changes are made and the analysis is rerun. A 9% reduction in the stress concentration is observed. Predicted and actual contact pressure histories are shown in Figure 9. The difference between the predicted and the actual results is due to the nonlinear dependence of the design response on the design parameter. However, the rerun confirms the prediction that the proposed design is more robust, with a possibly suboptimal wiping pressure.