Contact pressure definition

The contact modeling capabilities in Abaqus allow access to a library of “surface constitutive models.” Part of this library in Abaqus/Standard is the definition of the contact pressure between two surfaces at a point, $p$ , as a function of the “overclosure,” $h$ , of the surfaces (the interpenetration of the surfaces). Two models for $p = p (h)$ are provided as described below.

This page discusses:

Hard contact
Softened contact defined with an exponential pressure-overclosure relationship
Softened contact defined with a tabular pressure-overclosure relationship
Softened contact defined with a linear pressure-overclosure relationship
Softened contact implementation
Viscous damping option

Hard contact

In this case

\begin{matrix} p & = 0 for h < 0 (open), and \\ h & = 0 for p > 0 (closed) . \end{matrix}

The contact constraint is enforced with a Lagrange multiplier representing the contact pressure in a mixed formulation. The virtual work contribution is

δ Π = δ p h + p δ h,

and the linearized form of the contribution is

d δ Π = δ p d h + d p δ h .

Softened contact defined with an exponential pressure-overclosure relationship

This model provides an exponential $p$ – $h$ relationship, as shown in Figure 1.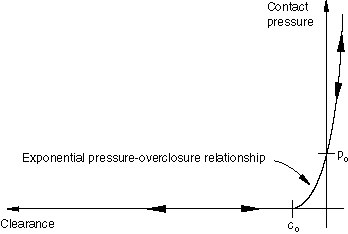

The user defines an initial contact distance, $c$ , and a typical pressure value, $p^{o}$ , which is the pressure value at zero overclosure ( $h = 0$ ). Then, we define


$p = 0$	for $h \leq - c$ ,
$p = \frac{p^{o}}{(\exp (1) - 1)} [(\frac{h}{c} + 1) (\exp (\frac{h}{c} + 1) - 1)]$	for $h > - c$ ,

and


$\frac{d p}{d h} = 0$	for $h \leq - c$ ,
$\frac{d p}{d h} = \frac{p^{o}}{(\exp (1) - 1)} [\frac{1}{c} (\frac{h}{c} + 2) \exp (\frac{h}{c} + 1) - \frac{1}{c}]$	for $h > - c$ .

Softened contact defined with a tabular pressure-overclosure relationship

The pressure-overclosure ( $p$ - $h$ ) relationship can be entered directly in tabular form as shown in Figure 2.

Softened contact defined with a linear pressure-overclosure relationship

The linear pressure-overclosure relationship is similar to the tabular relationship except that the linear form requires only a single value to be input to define the slope and the curve always passes through the origin.

Softened contact implementation

A mixed formulation is used because the exponential stiffness associated with softened contact tends to slow down convergence or, due to the development of excessive contact stresses, may cause divergence. For the mixed formulation the virtual work contribution is

\begin{matrix} (1) & δ Π = δ p (h - \bar{h}) + p δ h, \end{matrix}

where $p$ is the contact pressure, $h$ is the actual overclosure, and $\bar{h} (p)$ is the overclosure associated with the contact pressure, $p$ . A local Newton loop is used to calculate $\bar{h}$ for the current value of $p$ . The linearized form of this contribution is

\begin{matrix} (2) & d δ Π = δ p d h + d p δ h - \frac{d \bar{h}}{d p} δ p d p, \end{matrix}

where $d \bar{h} / d p = {(d p / d \bar{h})}^{- 1}$ is evaluated for the overclosure $\bar{h}$ . Since there is no term involving $δ h d h$ , there is a zero on the diagonal of the Jacobian. A zero on the diagonal is not desirable because it may lead to equation solver problems if a rigid body mode is constrained only by contact elements. Hence, a small reference stiffness $k_{0}$ is introduced by splitting the contact pressure as follows:

p = q + k_{0} (h + c) and δ p = δ q + k_{0} δ h,

where $q$ is a Lagrange multiplier and $k_{0}$ is a small reference stiffness (see Figure 1):

k_{0} = {\frac{d p}{d h} |}_{h = - 0.9999 c} .

Substituting for the pressure $p$ in Equation 1 and Equation 2, we obtain

\begin{matrix} (3) & δ Π = δ q (h - \bar{h}) + δ h [k_{0} (h - \bar{h}) + q + k_{0} (h + c)] \end{matrix}

and

\begin{matrix} (4) & d δ Π = δ q (d h - d \bar{h}) + δ h [k_{0} (d h - d \bar{h}) + d q + k_{0} d h] . \end{matrix}

Further,

d \bar{h} = \frac{d \bar{h}}{d p} d p = \frac{d \bar{h}}{d p} (d q + k_{0} d h) .

Therefore, substituting for $d \bar{h}$ in Equation 4,

d δ Π = δ q [(1 - \frac{d \bar{h}}{d p} k_{0}) d h - \frac{d \bar{h}}{d p} d q] + δ h [(2 - \frac{d \bar{h}}{d p} k_{0}) k_{0} d h + (1 - \frac{d \bar{h}}{d p} k_{0}) d q] .

Thus, the corresponding system of equations in matrix form is

[\begin{matrix} (2 - \frac{d \bar{h}}{d p} k_{0}) k_{0} & 1 - \frac{d \bar{h}}{d p} k_{0} \\ 1 - \frac{d \bar{h}}{d p} k_{0} & - \frac{d \bar{h}}{d p} \end{matrix}] {\begin{matrix} d h \\ d q \end{matrix}} = - {\begin{matrix} q + k_{0} (h + c) + k_{0} (h - \bar{h}) \\ h - \bar{h} \end{matrix}} .

In the mixed formulation the difference between the actual and the calculated overclosure $h - \bar{h}$ will go to zero as part of the iterative solution process. The difference must be sufficiently small to obtain an accurate solution. The admissible error in $h - \bar{h}$ is set to $0.005 c$ for $p \geq p^{0}$ . For $0 \leq p \leq p^{0}$ the admissible error is interpolated linearly between $0.005 c$ and $0.1 c$ , where $0.1 c$ represents the tolerance level at $p = 0.0$ ; alternatively, the tolerances can be specified by the user as part of the solution controls.

Viscous damping option

In addition to the surface constitutive models described above, where the contact pressure is a function of the surface overclosure, Abaqus/Standard allows for the definition of a “viscous” pressure that is proportional to the relative velocity, $\dot{h}$ , at which the surfaces approach or separate from each other. This option is intended for the regularization of snap-through problems involving contact where convergence difficulties arise due to the sudden violation of contact constraints.

The damping pressure, $f$ , is given by

f = f (h, \dot{h}) = μ (h) \dot{h},

where $μ$ is the damping coefficient. This coefficient is specified as a function of the overclosure, $h$ , as follows:

μ (h) = {\begin{matrix} 0 & for h < - c_{0} \\ μ_{0} (h + c_{0}) / (1 - η) c_{0} & for - c_{0} \leq h < - η c_{0}, \\ μ_{0} & for h \geq - η c_{0} \end{matrix}

where $μ_{0}$ is the value of the damping coefficient at zero overclosure and $η$ is the fraction of the overclosure interval $[- c_{0}, 0]$ over which the damping coefficient is equal to $μ_{0}$ .

The virtual work contribution associated with the damping pressure is

δ Π = f δ h .

The contribution to the stiffness matrix for the Newton solution is given by the linearized form of the virtual work contribution:

\begin{matrix} d δ Π & = δ h d f = δ h (\frac{\partial f}{\partial h} + \frac{\partial f}{\partial \dot{h}} \frac{\partial \dot{h}}{\partial h}) d h \\ ​ = δ h (\frac{d μ}{d h} \dot{h} + μ \frac{\partial \dot{h}}{\partial h}) d h, \end{matrix}

where

\frac{d μ}{d h} = {\begin{matrix} 0 & for h < - c_{0} \\ μ_{0} / (1 - η) c_{0} & for - c_{0} \leq h < - η c_{0} . \\ 0 & for h \geq - η c_{0} \end{matrix}

In static analysis the velocity is defined as the displacement increment divided by the time increment. Therefore, $\dot{h} = Δ h / Δ t$ , and the stiffness contribution reduces to

d δ Π = δ h (\frac{d μ}{d h} \frac{Δ h}{Δ t} + \frac{μ}{Δ t}) d h .

The previous expression also applies to dynamics if the backward Euler time integration operator is used. In the case of dynamics with the Hilber-Hughes-Taylor time integration operator, the stiffness contribution can be written as

d δ Π = δ h (\frac{d μ}{d h} \dot{h} + \frac{γ μ}{β Δ t}) d h,

where $γ$ and $β$ are the Hilber-Hughes-Taylor time integration operator parameters. The viscous damping option cannot be used in a Riks analysis since velocity is not defined.