Cylinder subjected to asymmetric pressure loads: CAXA elements

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

Elements tested
Problem description
Results and discussion
Input files
Figures

ProductsAbaqus/Standard

Elements tested

CAXA4n

CAXA4Rn

CAXA8n

CAXA8Rn

(n = 1, 2, 3, 4)

Problem description

A hollow cylinder of circular cross-section, inner radius $R_{i}$ , outer radius $R_{o}$ , and length $2 L$ is subjected to both internal and external pressure loads that are asymmetric. The pressure stresses take the following forms: $σ_{r r} = - p \cos θ$ at $r = R_{o}$ and $σ_{r r} = - \frac{R_{o}}{R_{i}} p \cos θ$ at $r = R_{i}$ , where p is a pressure value and r and $θ$ are the cylindrical coordinates. Assuming plane strain conditions and a linear elastic material with Young's modulus E and Poisson's ratio $ν$ , the small-displacement solutions for stress and displacement are as follows:

$\begin{matrix} σ_{r r} & = A [r + \frac{R_{i}^{2} R_{o}^{2}}{r^{3}} + \frac{(3 - 2 ν)}{(1 - 2 ν)} \frac{(R_{o}^{2} + R_{i}^{2})}{r}] \cos θ \\ σ_{θ θ} & = A [3 r - \frac{R_{i}^{2} R_{o}^{2}}{r^{3}} - \frac{(R_{o}^{2} + R_{i}^{2})}{r}] \cos θ \\ σ_{z z} & = ν (σ_{r r} + σ_{θ θ}) \\ σ_{r θ} & = A [r + \frac{R_{i}^{2} R_{o}^{2}}{r^{3}} - \frac{(R_{o}^{2} + R_{i}^{2})}{r}] \sin θ \\ u_{r} & = \frac{1 + ν}{2 E} A [(1 - 4 ν) r^{2} - \frac{R_{i}^{2} R_{o}^{2}}{r^{2}} + 2 \frac{(3 - 4 ν)}{(1 - 2 ν)} (R_{o}^{2} + R_{i}^{2}) \ln r] \cos θ \\ u_{θ} & = \frac{1 + ν}{2 E} A [(5 - 4 ν) r^{2} - \frac{R_{i}^{2} R_{o}^{2}}{r^{2}} - 2 \frac{(3 - 4 ν)}{(1 - 2 ν)} (R_{o}^{2} + R_{i}^{2}) \ln r - 2 \frac{(R_{o}^{2} + R_{i}^{2})}{(1 - 2 ν)}] \sin θ, \end{matrix}$

where

$A = - (1 - 2 ν) \frac{R_{o} p}{4 (1 - ν) (R_{o}^{2} + R_{i}^{2})} .$

Only a slice of the cylinder is considered. Plane strain conditions are applied by setting $u_{z} = $ 0 everywhere. In the r-direction 10 elements are used in the second-order element models. In models using the first-order elements, 20 and 40 elements are used in the full- and reduced-integration models, respectively.

Material:

Linear elastic, Young's modulus = 30 × 10⁶, Poisson's ratio = 0.3.

Boundary conditions:

$u_{z} = $ 0 everywhere; $u_{r} = $ −9.9854 × 10⁻⁴ at $r = R_{i}$ and $θ = $ 0°, as obtained from the equation for $u_{r}$ above. These constraints eliminate the rigid body motions in the global z- and x-directions, respectively.

Loading:

The asymmetric pressure loads are prescribed by applying the appropriate nonuniform distributed load types on the inside and outside surfaces of the cylinder and defining the pressure stress equations for $σ_{r r}$ in user subroutine DLOAD. In the user subroutine, the $θ$ value at each integration point, which is stored in COORDS(3), is expressed in degrees.

Results and discussion

The analytical solution and the Abaqus results for the CAXA8n, CAXA8Rn, CAXA4n, and CAXA4Rn (n = 1, 2, 3 or 4) elements are tabulated below for a cylinder with these parameters: $L = $ 6, $R_{i} = $ 2, $R_{o} = $ 6, and $P = $ 10 × 10³. The output locations are at points $A = (R_{i}, z, 0)$ and $C = (R_{o}, z, 0)$ on the $θ = $ 0° plane, where z can be any value along lines $A A$ and $C C$ in the figure shown on the previous page since the solution is independent of z, and at points E and G, which are at the corresponding locations on the $θ = $ 180° plane. The solutions predicted by Abaqus agree well with the exact solution. Closer agreement is anticipated if a denser mesh is used.


Variable	Exact	CAXA8n	CAXA8Rn	CAXA4n	CAXA4Rn
$σ_{r r}$ at A	−30000.0	−29610.0	−29760.0	−28617.0	−29132.0
$σ_{z z}$ at A	−7890.4	−7702.7	−7849.6	−7885.1	−7722.9
$σ_{θ θ}$ at A	6089.6	6268.2	5973.4	6034.6	5729.2
$σ_{r θ}$ at A	0.0	0.0	0.0	0.0	0.0
$u_{r}$ at A	−9.9854 × 10⁻⁴	−9.9854 × 10⁻⁴	−9.9854 × 10⁻⁴	−9.9854 × 10⁻⁴	−9.9854 × 10⁻⁴
$σ_{r r}$ at C	−10000.0	−9988.9	−9992.4	−10101.0	−10205.0
$σ_{z z}$ at C	−3969.9	−3964.4	−3967.9	−3952.2	−3978.2
$σ_{θ θ}$ at C	−2029.9	−2024.3	−2031.5	−2013.4	−1902.1
$σ_{r θ}$ at C	0.0	0.0	0.0	0.0	0.0
$u_{r}$ at C	−2.9222 × 10⁻³	−2.9222 × 10⁻³	−2.9222 × 10⁻³	−2.9207 × 10⁻³	−2.9221 × 10⁻³
$σ_{r r}$ at E	30000.0	29610.0	29760.0	28617.0	29132.0
$σ_{z z}$ at E	7890.4	7702.7	7849.6	7885.1	7722.9
$σ_{θ θ}$ at E	−6089.6	−6268.2	−5973.4	−6034.6	−5729.2
$σ_{r θ}$ at E	0.0	0.0	0.0	0.0	0.0
$u_{r}$ at E	9.9854 × 10⁻⁴	9.9854 × 10⁻⁴	9.9854 × 10⁻⁴	9.9854 × 10⁻⁴	9.9854 × 10⁻⁴
$σ_{r r}$ at G	10000.0	9988.9	9992.4	10101.0	10067.0
$σ_{z z}$ at G	3969.9	3964.4	3967.9	3952.2	3978.2
$σ_{θ θ}$ at G	2029.9	2024.3	2031.5	2013.4	1987.9
$σ_{r θ}$ at G	0.0	0.0	0.0	0.0	0.0
$u_{r}$ at G	2.9222 × 10⁻³	2.9222 × 10⁻³	2.9222 × 10⁻³	2.9207 × 10⁻³	2.9221 × 10⁻³

Note:

The results are independent of n, the number of Fourier modes. The $u_{θ}$ variable is not compared, since $u_{θ}$ is treated as an internal variable in these elements and is not available for output. The accuracy of $u_{θ}$ may be assumed to be comparable to the accuracy of $u_{r}$ .

Figure 1 through Figure 4 show plots of the undeformed mesh, the deformed mesh, the contours of $σ_{r r}$ , and the contours of $u_{r}$ , respectively, for the CAXA8R3 model.

Input files

ecnssfsm.inp: CAXA41 elements.
ecnssfsm.f: User subroutine DLOAD used in ecnssfsm.inp.
ecntsfsm.inp: CAXA42 elements.
ecntsfsm.f: User subroutine DLOAD used in ecntsfsm.inp.
ecnusfsm.inp: CAXA43 elements.
ecnusfsm.f: User subroutine DLOAD used in ecnusfsm.inp.
ecnvsfsm.inp: CAXA44 elements.
ecnvsfsm.f: User subroutine DLOAD used in ecnvsfsm.inp.
ecnssrsm.inp: CAXA4R1 elements.
ecnssrsm.f: User subroutine DLOAD used in ecnssrsm.inp.
ecntsrsm.inp: CAXA4R2 elements.
ecntsrsm.f: User subroutine DLOAD used in ecntsrsm.inp.
ecnusrsm.inp: CAXA4R3 elements.
ecnusrsm.f: User subroutine DLOAD used in ecnusrsm.inp.
ecnvsrsm.inp: CAXA4R4 elements.
ecnvsrsm.f: User subroutine DLOAD used in ecnvsrsm.inp.
ecnwsfsm.inp: CAXA81 elements.
ecnwsfsm.f: User subroutine DLOAD used in ecnwsfsm.inp.
ecnxsfsm.inp: CAXA82 elements.
ecnxsfsm.f: User subroutine DLOAD used in ecnxsfsm.inp.
ecnysfsm.inp: CAXA83 elements.
ecnysfsm.f: User subroutine DLOAD used in ecnysfsm.inp.
ecnzsfsm.inp: CAXA84 elements.
ecnzsfsm.f: User subroutine DLOAD used in ecnzsfsm.inp.
ecnwsrsm.inp: CAXA8R1 elements.
ecnwsrsm.f: User subroutine DLOAD used in ecnwsrsm.inp.
ecnxsrsm.inp: CAXA8R2 elements.
ecnxsrsm.f: User subroutine DLOAD used in ecnxsrsm.inp.
ecnysrsm.inp: CAXA8R3 elements.
ecnysrsm.f: User subroutine DLOAD used in ecnysrsm.inp.
ecnzsrsm.inp: CAXA8R4 elements.
ecnzsrsm.f: User subroutine DLOAD used in ecnzsrsm.inp.

Figures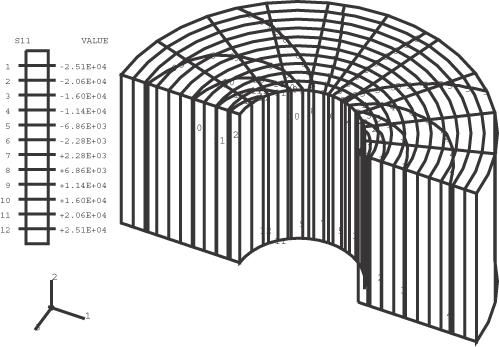